
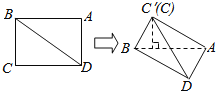
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() ,
,![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】泰兴机械厂生产一种木材旋切机械,已知生产总利润c元与生产量x台之间的关系式为c(x)=-2x2+7 000x+600.
(1)求产量为1 000台的总利润与平均利润;
(2)求产量由1 000台提高到1 500台时,总利润的平均改变量;
(3)求c′(1 000)与c′(1 500),并说明它们的实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)= ![]() ,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
②函数f(x)是偶函数;
③任意一个非零有理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC为等边三角形.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点 .
.
(1)求椭圆的方程;
(2)设椭圆与![]() 轴的非负半轴交于点
轴的非负半轴交于点![]() ,过点
,过点![]() 作互相垂直的两条直线,分别交椭圆于
作互相垂直的两条直线,分别交椭圆于![]() 两点,连接
两点,连接![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示. 
(1)求图中x的值,并根据频率分布直方图估计这500名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
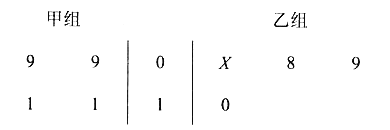
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com