
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 的形状.
的形状.
(1)根据两角和差的余弦公式可以得到结论,
(2) 为直角三角形
为直角三角形
解析试题分析:解:解法一:(Ⅰ)因为 , ①
, ① , ② 2分
, ② 2分
①-② 得 . ③ 3分
. ③ 3分
令 有
有 ,
,
代入③得 . 6分
. 6分
(Ⅱ)由二倍角公式, 可化为
可化为 , 8分
, 8分
即 . 9分
. 9分
设 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为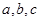 ,
,
由正弦定理可得 11分
11分
根据勾股定理的逆定理知 为直角三角形. 12分
为直角三角形. 12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的结论和二倍角公式,  可化为
可化为 , 8分
, 8分
因为A,B,C为 的内角,所以
的内角,所以 ,
,
所以 .
.
又因为 ,所以
,所以 ,
,
所以 .
.
从而 . 10分
. 10分
又因为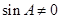 ,所以
,所以 ,即
,即 .
.
所以 为直角三角形. 12分
为直角三角形. 12分
考点:解三角形,两角和差公式
点评:主要是考查了运用两角和差的公式推理论证表达式以及运用二倍角公式来得到三角形定形,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)已知函数 ,
,
(1)求函数f (x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对应边分别为 、b、c,且
、b、c,且 ,若向量
,若向量 共线,求
共线,求 、b的值;
、b的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com