
(本题满分12)
已知x=1是函数f(x)=m![]() -3(m+1)
-3(m+1)![]() +nx+1的一个极值点,其中m,n
+nx+1的一个极值点,其中m,n![]()
![]() R,m<0.
R,m<0.
(Ⅰ)求m与n的关系表达式; (Ⅱ)求f(x)的单调区间;
(Ⅲ)当x![]()
![]() 时,函数y=f(x)的图像上任意一点的切线斜率恒大于3m,求m的取值范围。
时,函数y=f(x)的图像上任意一点的切线斜率恒大于3m,求m的取值范围。
解:
(I)f′(x)= 3m![]() -6(m+1)x+n 因为x=1是f(x)的一个极值点,所以f′(1)=0,即 3m-6(m+1)+n=0 所以 n=3m+6. ………………………………3分
-6(m+1)x+n 因为x=1是f(x)的一个极值点,所以f′(1)=0,即 3m-6(m+1)+n=0 所以 n=3m+6. ………………………………3分
(Ⅱ) 由(I)知, f′(x)= 3m![]() -6(m+1)x+3m+6=3m(x-1)[x-(1+
-6(m+1)x+3m+6=3m(x-1)[x-(1+![]() )].
)].
当m<0时,有1>1+![]() .
.
当x变化时,f(x)与f′(x)的变化如下表:
| x | (-∞,1+ | 1+ | (1+ | 1 | (1,∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
由表知,当m<0时,f(x)在(-∞,1+![]() )内单调递减,在(1+
)内单调递减,在(1+![]() ,1)内单调递增,在(1,∞)内单调递减。 ………………………………7分
,1)内单调递增,在(1,∞)内单调递减。 ………………………………7分
(Ⅲ)解法一 由已知条件,得f′(x)﹥3m,即 m![]() -2(m+1)x+2 > 0.
-2(m+1)x+2 > 0.
因为 m < 0,所以 ![]() -
-![]() (m+1)+
(m+1)+![]() < 0,
< 0,
即 ![]() -2(1+
-2(1+![]() )x+
)x+![]() < 0 , x
< 0 , x![]() [-1,1] ①
[-1,1] ①
设g(x)= ![]() -2(1+
-2(1+![]() )x+
)x+![]() ,其函数图像的开口向上。由题意①式恒成立,
,其函数图像的开口向上。由题意①式恒成立,
所以{![]()
![]() {
{![]()
![]() {
{![]()
![]() -
-![]()
又m < 0,所以 -![]() < 0,
< 0,
故m的取值范围是 -![]() < 0. ………………………………12分
< 0. ………………………………12分
解法二 由已知条件,得f′(x)﹥3m,即 3m(x-1)[x-(1+![]() )] > 3m.
)] > 3m.
因为m< 0,所以(x-1)[x-(1+![]() )]< 1 ②
)]< 1 ②
(ⅰ)x=1时,②式化为0 < 1,恒成立,所以m< 0.
(ⅱ)x≠1时,因为 x![]() [-1,1],所以 -2≤x-1<0.
[-1,1],所以 -2≤x-1<0.
②式化为 ![]() <(x-1)-
<(x-1)-![]() , 令t=x-1,则t
, 令t=x-1,则t![]() [-2,0〕.
[-2,0〕.
记 g(t)=t-![]() , 则 g(t)在区间[-2,0〕上是单调增函数,
, 则 g(t)在区间[-2,0〕上是单调增函数,
所以 ![]() =g(-2)=-2-
=g(-2)=-2-![]() =-
=-![]() .
.
由②式恒成立,必有 ![]() < -
< -![]()
![]() -
-![]() < m.
< m.
又m < 0,综合(ⅰ),(ⅱ)知 -![]() < 0. ………………………………12分
< 0. ………………………………12分


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
(本题满分12分)已知![]() 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设![]() ,
,![]() ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求![]() 和
和![]() 的定义域;(2)如果
的定义域;(2)如果![]() 和
和![]() 两个函数的定义域的交集为非空集合,求c的取值范围;(3)当
两个函数的定义域的交集为非空集合,求c的取值范围;(3)当![]() 在其定义域内是奇函数,又是增函数时,求使
在其定义域内是奇函数,又是增函数时,求使![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一寒假作业1数学试卷(解析版) 题型:解答题
(本题满分12分)
已知直线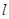 经过直线
经过直线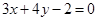 与直线
与直线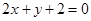 的交点
的交点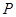 ,且垂直于直线
,且垂直于直线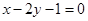 .
.
(Ⅰ)求直线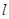 的方程;
的方程;
(Ⅱ)求直线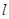 与两坐标轴围成的三角形的面积
与两坐标轴围成的三角形的面积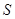 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知函数f(x)=x3+ax2+(a+6)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是3,求a,b的值;
(2) 若f(x)为R上的单调递增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省高三第四次模拟考试理科数学 题型:解答题
(.(本题满分12分)
已知二次函数 和“伪二次函数”
和“伪二次函数”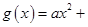
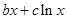 (
(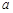 、
、 、
、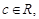
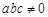 ),
),
(I)证明:只要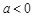 ,无论
,无论 取何值,函数
取何值,函数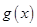 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数 图象上任意取不同两点
图象上任意取不同两点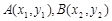 ,线段
,线段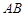 中点的横坐标为
中点的横坐标为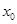 ,记直线
,记直线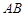 的斜率为
的斜率为 ,
,
(i)求证: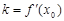 ;
;
(ii)对于“伪二次函数”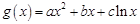 ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com