
分析 由函数的解析式判断单调性,求出f(2),f(3)的值,可得f(2)•f(3)<0,再利用函数的零点的判定定理可得函数f(x)=$\frac{5}{{2}^{x}}$-log2x的零点所在的区间
解答 解:∵函数f(x)=$\frac{5}{{2}^{x}}$-log2x,
∴可判断函数单调递减
∵f(2)=$\frac{5}{4}-lo{g}_{2}2$=$\frac{1}{4}$>0,f(3)=$\frac{5}{8}-lo{g}_{2}3$<0,
∴f(2)•f(3)<0,
根据函数的零点的判定定理可得:
函数f(x)=$\frac{5}{{2}^{x}}$-log2x的零点所在的区间是 (2,3),
n的值为:2.
故答案为:2.
点评 本题主要考查函数的零点的判定定理的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 球O与棱长为a的正方体ABCD-A1B1C1D1的各个面均相切,如图,用平平行于底面的平面截去长方体A2B2C2D2-A1B1C1D1,得到截面A2B2C2D2,且A2A=$\frac{3}{4}$a,现随机向截面A2B2C2D2上撒一粒黄豆,则黄豆落在截面中的圆内的概率为( )
球O与棱长为a的正方体ABCD-A1B1C1D1的各个面均相切,如图,用平平行于底面的平面截去长方体A2B2C2D2-A1B1C1D1,得到截面A2B2C2D2,且A2A=$\frac{3}{4}$a,现随机向截面A2B2C2D2上撒一粒黄豆,则黄豆落在截面中的圆内的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{3π}{16}$ | C. | $\frac{π}{4}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
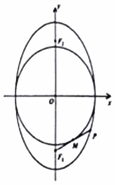 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
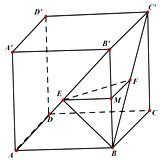 如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.
如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1]∪[1,+∞) | C. | (-1,0)∪(0,1) | D. | [-1,0)∪(0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com