
【题目】已知圆![]() ,直线
,直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,点
,点![]() 是线段
是线段![]() 的中点。
的中点。
(1)求直线![]() 的方程;
的方程;
(2)是否存在与直线![]() 平行的直线
平行的直线![]() ,使得
,使得![]() 与与圆
与与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 不经过点
不经过点![]() ,且
,且![]() 的面积
的面积![]() 最大?若存在,求出
最大?若存在,求出![]() 的方程及对应的
的方程及对应的![]() 的面积S;若不存在,请说明理由。
的面积S;若不存在,请说明理由。
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,为了打赢疫情防控阻击战,我们执行了延长假期政策,在延长假期面前,我们“停课不停学”,河南省教育厅组织部分优秀学校的优秀教师录播《名师同步课堂》,我校高一年级要在甲、乙、丙、丁、戊5位数学教师中随机抽取3人参加录播课堂,则甲、乙两位教师同时被选中的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究黏虫孵化的平均温度![]() (单位:
(单位: ![]() )与孵化天数
)与孵化天数![]() 之间的关系,某课外兴趣小组通过试验得到如下6组数据:
之间的关系,某课外兴趣小组通过试验得到如下6组数据:
组号 | 1 | 2 | 3 | 4 | 5 | 6 |
平均温度 | 15.3 | 16.8 | 17.4 | 18 | 19.5 | 21 |
孵化天数 | 16.7 | 14.8 | 13.9 | 13.5 | 8.4 | 6.2 |
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:
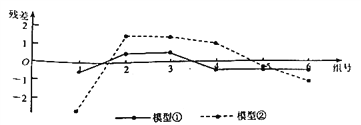
经计算得![]() ,
,
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?(给出判断即可,不必说明理由)
(2)残差绝对值大于1的数据被认为是异常数据,需要剔除,剔除后应用最小二乘法建立![]() 关于
关于![]() 的线性回归方程.(精确到0.1)
的线性回归方程.(精确到0.1)
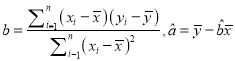 ,.
,.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,若函数
,若函数![]() 有三个不同的零点
有三个不同的零点![]() ,
,![]() ,
,![]() (其中
(其中![]() ),则
),则![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】如图: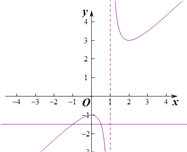

![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]()
![]() ,由
,由![]() 有三个不同的零点
有三个不同的零点
![]() ,如图
,如图
令![]()
![]()
得![]()
![]()
为满足有三个零点,如图可得
![]() ,
,![]()
![]()
![]()
点睛:本题考查了函数零点问题,先由导数求出两个函数的单调性,继而画出函数图像,再由函数的零点个数确定参量取值范围,将问题转化为函数的两根问题来求解,本题需要化归转化,函数的思想,零点问题等较为综合,有很大难度。
【题型】填空题
【结束】
17
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程组,解出即可;
的方程组,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用导数研究其单调性可得
, 利用导数研究其单调性可得
![]() ,
,
从而证明![]() .
.
试题解析:((1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;且
单调递增;且![]() ,
,
所以![]() 在
在![]() 上当单调递减,在
上当单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
故![]() ,
,
故![]() .
.
【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为![]() ,设∠AOE=
,设∠AOE=![]() ,探照灯O照射在长方形ABCD内部区域的面积为S.
,探照灯O照射在长方形ABCD内部区域的面积为S.
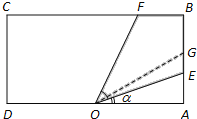
(1)当0≤![]()
![]() 时,写出S关于
时,写出S关于![]() 的函数表达式;
的函数表达式;
(2)若探照灯每9分钟旋转“一个来回”(OE自OA转到OC,再回到OA,称“一个来回”,忽略OE在OA及OC反向旋转时所用时间),且转动的角速度大小一定,设AB边上有一点G,且∠AOG![]() ,求点G在“一个来回”中,被照到的时间.
,求点G在“一个来回”中,被照到的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20海里的C处的乙船,现乙船朝北偏东![]() 的方向即沿直线CB前往B处救援,则
的方向即沿直线CB前往B处救援,则![]() 等于 ( )
等于 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com