
【题目】已知函数fn(x)= ![]() (n∈N*),关于此函数的说法正确的序号是
(n∈N*),关于此函数的说法正确的序号是
①fn(x)(n∈N*)为周期函数;②fn(x)(n∈N*)有对称轴;③( ![]() ,0)为fn(x)(n∈N*)的对称中心:④|fn(x)|≤n(n∈N*).
,0)为fn(x)(n∈N*)的对称中心:④|fn(x)|≤n(n∈N*).
【答案】①②④
【解析】解:∵函数fn(x)= ![]() (n∈N*),
(n∈N*),
∴①fn(x+2π)=fn(x)(n∈N*),fn(x为周期函数,正确;
②fn(﹣x)= ![]() =
= ![]() ,fn(x)=
,fn(x)= ![]() (n∈N*)是偶函数,∴fn(x)=
(n∈N*)是偶函数,∴fn(x)= ![]() (n∈N*)有对称轴,正确;
(n∈N*)有对称轴,正确;
③n为偶数时,fn( ![]() )=
)= ![]() =0,∴(
=0,∴( ![]() ,0)为fn(x)(n∈N*)的对称中心,不正确;
,0)为fn(x)(n∈N*)的对称中心,不正确;
④∵|sinnx|≤|nsinx|,∴|fn(x)|≤n(n∈N*),正确.
所以答案是:①②④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 .
,AB为椭圆的一条弦(不经过原点),直线y=kx(k>0)经过弦AB的中点,与椭圆C交于P,Q两点,设直线AB的斜率为k1 . 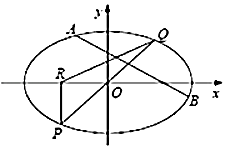
(1)若点Q的坐标为(1, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(2)求证:k1k为定值;
(3)过P点作x轴的垂线,垂足为R,若直线AB和直线QR倾斜角互补.若△PQR的面积为2 ![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() ,设
,设![]() ,记使得
,记使得![]() 成立的
成立的![]() 的最大值为
的最大值为![]() .
.
(![]() )设数列
)设数列![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,写出
,写出![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若
)若![]() 为等比例数列,且
为等比例数列,且![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x-3)2+(y-4)2=1,设点P是圆C上的动点.记d=|PB|2+|PA|2,其中A(0,1),B(0,-1),则d的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第 ![]() 个图形包含
个图形包含 ![]() 个小正方形.
个小正方形.
(Ⅰ)求出 ![]() ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出 ![]() 与
与 ![]() 的关系式,并根据你得到的关系式求
的关系式,并根据你得到的关系式求 ![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com