
【题目】设椭圆M: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,点A(a,0),B(0,﹣b),原点O到直线AB的距离为
,点A(a,0),B(0,﹣b),原点O到直线AB的距离为 ![]() .
.
(Ⅰ)求椭圆M的方程;
(Ⅱ)设直线l:y=2x+m与椭圆M相交于C、D不同两点,经过线段CD上点E的直线与y轴相交于点P,且有 ![]() =0,|
=0,| ![]() |=|
|=| ![]() |,试求△PCD面积S的最大值.
|,试求△PCD面积S的最大值.
【答案】解:(Ⅰ)由 ![]() 得a=
得a= ![]()
可得直线AB的方程为 ![]() ,于是
,于是  ,
,
得b= ![]() ,b2=2,a2=4,所以椭圆M的方程为
,b2=2,a2=4,所以椭圆M的方程为 ![]()
(Ⅱ)设C(x1 , y1),D(x2 , y2),由方程组 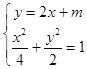 ,
,
得9x2+8mx+2m2﹣4=0,
所以有 ![]() ,
, ![]() ,且△≥0,即m2≤18.
,且△≥0,即m2≤18.![]()
= ![]()
= ![]()
= ![]()
= ![]() .
.
因为 ![]() =0,
=0,
所以 ![]() ,
,
又| ![]() |=|
|=| ![]() |,
|,
所以E是线段CD的中点,
点E的坐标为 ![]() ,即E的坐标是
,即E的坐标是 ![]() ,
,
因此直线PE的方程为y=﹣ ![]() ,得点P的坐标为(0,﹣
,得点P的坐标为(0,﹣ ![]() ),
),
所以|PE|= 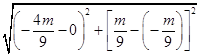
= ![]() .(2分)
.(2分)
因此 ![]()
= ![]() .
.
所以当m2=9,即m=±3时,S取得最大值,最大值为 ![]() .
.
【解析】(Ⅰ)由 ![]() 得a=
得a= ![]() .可得直线AB的方程为
.可得直线AB的方程为 ![]() ,于是
,于是 ![]() ,由此能够求出椭圆M的方程.(Ⅱ)设C(x1 , y1),D(x2 , y2),由方程组
,由此能够求出椭圆M的方程.(Ⅱ)设C(x1 , y1),D(x2 , y2),由方程组 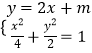 ,得9x2+8mx+2m2﹣4=0,所以有
,得9x2+8mx+2m2﹣4=0,所以有 ![]() ,
, ![]() ,且△≥0,即m2≤18.
,且△≥0,即m2≤18. ![]() =
= ![]() .由
.由 ![]() ,E是线段CD的中点,由此能求出S的最大值.
,E是线段CD的中点,由此能求出S的最大值.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的正视图是( ) 
A.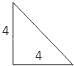
B.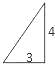
C.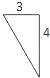
D.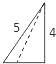
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从一批该零件巾随机抽取20个,对其等级进行统计分析,得到频率分布表如下
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级恰好相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,
,
(1)若a=﹣1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
(3)若f(x)的值域是(0,+∞),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形DCFE折起,使得平面DCFE⊥平面ABCD. 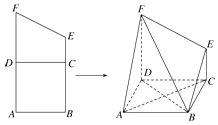
(1)证明:AC∥平面BEF;
(2)求三棱锥D﹣BEF的体积;
(3)求直线AF与平面BDF所求的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com