
【题目】已知函数![]() ,若对任意的
,若对任意的![]() 且
且![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线经过点
的抛物线经过点![]() 和
和![]() .
.
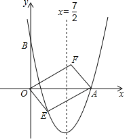
(1)求抛物线解析式及顶点坐标;
(2)设点![]() 是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有![]() 的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式与数据![]() 对应
对应![]() ,
,![]() 对应
对应![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
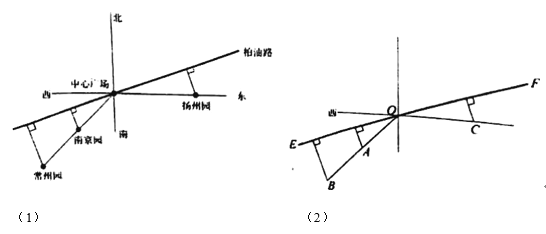
【题目】江苏省园博会有一中心广场,南京园,常州园都在中心广场的南偏西45°方向上,到中心广场的距离分别为![]() km,
km,![]() km;扬州园在中心广场的正东方向,到中心广场的距离为
km;扬州园在中心广场的正东方向,到中心广场的距离为![]() km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为
km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为![]() (
(![]() (0,
(0,![]() )),铺设三段鹅卵石路的总费用为y(万元).
)),铺设三段鹅卵石路的总费用为y(万元).
(1)求南京园到柏油路的最短距离![]() 关于
关于![]() 的表达式;
的表达式;
(2)求y的最小值及此时tan![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
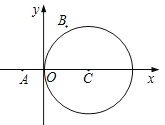
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
,![]() .
.
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com