已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若
=-4,则直线AB的斜率为( )
由题意可知直线的斜存在,故可设为k(k≠0)
∵抛物线 C:y
2=4x焦点F(1,0),准线x=-1,则直线AB的方程为y=k(x-1)
联立方程
可得k
2x
2-2(2+k
2)x+k
2=0
设A(x
1,y
1),B(x
2,y
2),则
x1+x2=,y
1+y
2=k(x
1+x
2-2)=
•k=
=(x1-1,y1),
=(x2-1,y2)∵
=-4,
∴
即
②
①②联立可得,
x2=,
y2=-•k=-,代入抛物线方程y
2=4x可得
=×4
∴9k
2=16
∴
k=±故选D
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
(2010•聊城一模)已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若
=-4,则直线AB的斜率为( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省芜湖市三校高二(上)期末数学试卷(文科)(解析版)
题型:选择题
已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若

,则直线AB的斜率为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2011年安徽省蚌埠二中高三最后模拟数学试卷(文科)(解析版)
题型:选择题
已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若

,则直线AB的斜率为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2010年广东省华南师大附中高三综合测试数学试卷(理科)(解析版)
题型:选择题
已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若

,则直线AB的斜率为( )
A.

B.

C.
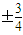
D.

查看答案和解析>>
科目:高中数学
来源:2010年山东省聊城市高考数学一模试卷(理科)(解析版)
题型:选择题
已知A、B为抛物线C:y
2=4x上的不同两点,F为抛物线C的焦点,若

,则直线AB的斜率为( )
A.

B.

C.

D.

查看答案和解析>>



 ,则直线AB的斜率为( )
,则直线AB的斜率为( )



 ,则直线AB的斜率为( )
,则直线AB的斜率为( )



 ,则直线AB的斜率为( )
,则直线AB的斜率为( )

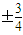

 ,则直线AB的斜率为( )
,则直线AB的斜率为( )


