
分析 (1)当0≤x<e时,求导函数,可得f(x)在区间[0,e]上的最大值;
(2)假设曲线y=f(x)上存在两点P、Q满足题设要求,则点P、Q只能在y轴两侧.设P、Q的坐标,由此入手能得到对任意给定的正实数a,曲线y=f(x)上存在两点P、Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
解答 解:(1)∵f(x)=$\left\{\begin{array}{l}{-{x}^{3}+{x}^{2},x<1}\\{alnx,x≥1}\end{array}\right.$,
当0≤x<1时,f′(x)=-3x2+2x=-3x(x-$\frac{2}{3}$),
令f'(x)>0,解得:0≤x<$\frac{2}{3}$,
令f′(x)<0,解得:$\frac{2}{3}$<x<1,
故f(x)在[0,$\frac{2}{3}$)递增,在($\frac{2}{3}$,1)递减,
而f($\frac{2}{3}$)=$\frac{4}{27}$,
∴f(x)在区间[0,1)上的最大值为$\frac{4}{27}$,
1≤x<e时,f(x)=alnx,f′(x)=$\frac{a}{x}$>0,
f(x)在[1,e]递增,f(x)max=f(e)=a≥1,
综上f(x)在[0,e]的最大值是a;
(2)曲线y=f(x)上存在两点P、Q满足题设要求,则点P,Q只能在y轴的两侧,
不妨设P(t,f(t))(t>0),则Q(-t,t3+t2),显然t≠1,
∵△POQ是以O为直角顶点的直角三角形,
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,即-t2+f(t)(t3+t2)=0.(1)
是否存在两点P、Q等价于方程(1)是否有解.
若0<t<1,则f(t)=-t3+t2,代入(1)式得,
-t2+(-t3+t2)(t3+t2)=0,即t4-t2+1=0,
而此方程无实数解,因此t>1.
∴f(t)=alnt,代入(1)式得,-t2+(alnt)(t3+t2)=0,
即$\frac{1}{a}$=(t+1)lnt. (*),
考察函数在h(x)=(x+1)lnx(x≥1),
则h′(x)=lnx+$\frac{1}{x}$+1>0,
∴h(x)在[1,+∞)上单调递增,∵t>1,∴h(t)>h(1)=0,
当t→+∞时,h(t)→+∞,∴h(t)的取值范围是(0,+∞).
∴对于a>0,方程(*)总有解,即方程(1)总有解.
因此对任意给定的正实数a,曲线y=f(x)上总存在两点P、Q,
使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
点评 本题考查导数知识的运用,考查学生分析解决问题的能力,考查学生的计算能力,综合性强.


科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③⑤ | C. | ①③④ | D. | ①②⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
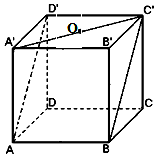
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
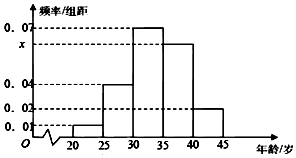 为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].
为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 42 | B. | 44 | C. | 46 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=45,p=$\frac{2}{3}$ | B. | n=45,p=$\frac{1}{3}$ | C. | n=90,p=$\frac{1}{3}$ | D. | n=90,p=$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com