已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2,则(x1-1)2+(x2-1)2的最小值是________.
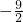
分析:由根与系数关系得出x
1+x
2=-2k,x
1•x
2=k
2+k+3,再将(x
1-1)
2+(x
2-1)
2化简为
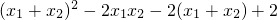
,代入可得.
解答:∵关于x的方程x
2+2kx+k
2+k+3=0的两根分别是x
1、x
2,
∴x
1+x
2=-2k,x
1•x
2=k
2+k+3,
(x
1-1)
2+(x
2-1)
2=
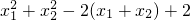
=
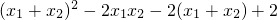
=(-2k)
2-2(k
2+k+3)-2(-2k)+2
=2k
2+2k-4=2
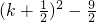
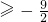
故答案为:
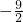
点评:本题考查根与系数的关系和配方法的应用,根与系数的关系是数学中的重点内容,此题进行配方是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案