
 正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.
正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高. 分析 画出图形,分别求出三棱台上下底面的中心到顶点和到对边的距离,再利用勾股定理求出棱台的侧棱长与斜高.
解答 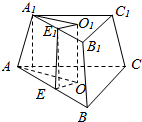 解:如图所示,
解:如图所示,
正三棱台ABC-A1B1C1中,高OO1=3,底面边长为A1B1=2,AB=4,
∴OA=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$AB=$\frac{4}{3}$$\sqrt{3}$,
O1A1=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$A1B1=$\frac{2}{3}$$\sqrt{3}$,
∴棱台的侧棱长为
AA1=$\sqrt{{3}^{2}{+(\frac{4}{3}\sqrt{3}-\frac{2}{3}\sqrt{3})}^{2}}$=$\frac{\sqrt{93}}{3}$;
又OE=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$AB=$\frac{2}{3}$$\sqrt{3}$,
O1E1=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$A1B1=$\frac{1}{3}$$\sqrt{3}$,
∴该棱台的斜高为
EE1=$\sqrt{{3}^{2}{+(\frac{2}{3}\sqrt{3}-\frac{1}{3}\sqrt{3})}^{2}}$=$\frac{2}{3}$$\sqrt{21}$.
点评 本题考查了求正三棱台的侧棱长与斜高的应用问题,也考查了计算能力的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2+3i | B. | -2-3i | C. | 4-3i | D. | 4+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an}是以q(q≠1)为公比的等比数列,则a1+a2+…+an=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$ | |
| B. | 若n∈N*,则cos$\frac{α}{2}$•cos$\frac{α}{{2}^{2}}$•cos$\frac{α}{{2}^{3}}$…cos$\frac{α}{{2}^{n}}$=$\frac{sinα}{{2}^{n}sin\frac{α}{{2}^{n}}}$ | |
| C. | 若n∈N*,则n2+3n+1是质数 | |
| D. | (n2-1)+22(n2-22)+…+n2(n2-n2)=$\frac{{n}^{2}(n-1)(n+1)}{4}$对任何n∈N*都成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{5}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com