
分析 (1)根据条件建立方程关系即可确定f(x)的解析式;
(2)根据函数单调性的定义即可判断f(x)的单调性并用定义证明;
(3)利用函数奇偶性和单调性之间的关系即mx-x>1-x2,即存在x∈[$\frac{1}{2}$,1]使mx-x>1-x2成立即-1≤mx-x≤1成立.
解答 解:(1)∵函数f(x)=$\frac{ax+b}{1+{x}^{2}}$是定义在[-1,1]上的奇函数,
∴b=0,f(x)=$\frac{ax}{1{+x}^{2}}$,而f($\frac{1}{3}$)=$\frac{3}{10}$,即$\frac{\frac{1}{3}a}{1+\frac{1}{9}}$=$\frac{3}{10}$,解得:a=1,
故f(x)=$\frac{x}{1{+x}^{2}}$;
(2)函数f(x)=$\frac{x}{1{+x}^{2}}$在[-1,1]上为增函数;
下证明:设任意x1,x2∈[-1,1]且x1<x2
则f(x1)-f(x2)=$\frac{{x}_{1}}{{{x}_{1}}^{2}+1}$-$\frac{{x}_{2}}{1{{+x}_{2}}^{2}}$=$\frac{{(x}_{1}{-x}_{2})(1{{-x}_{1}x}_{2})}{{{(x}_{1}}^{2}+1){{(x}_{2}}^{2}+1)}$,
因为x1<x2,所以x1-x2<0,又因为x1,x2∈[-1,1],所以1-x1x2>0
即$\frac{{(x}_{1}{-x}_{2})(1{{-x}_{1}x}_{2})}{{{(x}_{1}}^{2}+1){{(x}_{2}}^{2}+1)}$<0,即f(x1)<f(x2),
故函数f(x)在[-1,1]上为增函数;
(3)因为f(mx-x)+f(x2-1)>0,所以f(mx-x)>-f(x2-1),
即f(mx-x)>f(1-x2),
又由( II)函数y=f(x)在[-1,1]上为增函数,
所以mx-x>1-x2,即存在x∈[$\frac{1}{2}$,1]使mx-x>1-x2成立即-1≤mx-x≤1成立,
即存在x∈[$\frac{1}{2}$,1]使m>-x+$\frac{1}{x}$+1成立且1-$\frac{1}{x}$≤m≤1+$\frac{1}{x}$成立,
得:m>1且-1≤m≤2,
故实数m的所有可能取值{m|1<m≤2}.
点评 本题主要考查函数奇偶性和单调性的应用,以及函数单调性的证明,综合考查函数的性质,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
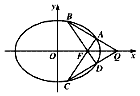 如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.
如图,过椭圆M:$\frac{{x}^{2}}{2}$+y2=1的右焦点F作直线交椭圆于A,C两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
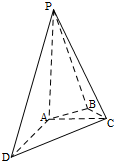 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3:\sqrt{10}$ | B. | $1:\sqrt{10}$ | C. | 1:2 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com