
【题目】如图,在空间直角坐标系O-xyz中,已知正四棱锥PABCD的高OP=2,点B,D和C,A分别在x轴和y轴上,且AB=![]() ,点M是棱PC的中点.
,点M是棱PC的中点.
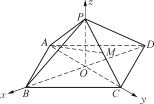
(1)求直线AM与平面PAB所成角的正弦值;
(2)求二面角A-PB-C的余弦值.
【答案】(1)![]() .(2)-
.(2)-![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 的坐标和平面PAB的一个法向量,再利用线线角的向量方法求解.
的坐标和平面PAB的一个法向量,再利用线线角的向量方法求解.
(2)由(1)知平面PAB的一个法向量,再求得平面PBC的一个法向量,利用面面角的向量方法求解.
(1)建立如图所示空间直角坐标系
记直线AM与平面PAB所成角为![]() ,
,
则A(0,-1,0),B(1,0,0),C(0,1,0),P(0,0,2),M![]() ,
,
则![]() =(1,1,0),
=(1,1,0),![]() =(0,-1,-2),
=(0,-1,-2),![]() =
=![]() .
.
设平面PAB的法向量为![]() =(x,y,z),
=(x,y,z),
所以 即
即![]()
令x=2,则y=-2,z=1,
所以平面PAB的一个法向量为![]() =(2,-2,1),
=(2,-2,1),
所以sinα=|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=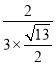 =
=![]() .
.
即直线AM与平面PAB所成角的正弦值为![]() .
.
(2)设平面PBC的法向量为![]() =(x1,y1,z1),
=(x1,y1,z1),![]() =(-1,1,0),
=(-1,1,0),![]() =(1,0,-2).
=(1,0,-2).
由 即
即
令x1=2,则y1=2,z1=1,所以平面PBC的一个法向量为![]() =(2,2,1),
=(2,2,1),
所以cos〈![]() ,
,![]() 〉=
〉=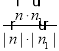 =
=![]() =
=![]() .
.
由图可知二面角A-PB-C为钝角,故二面角的余弦值为-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2017年3月18日,国务院办公厅发布了《生活垃圾分类制度实施方案》,我市环保部门组织了一次垃圾分类知识的网络问卷调查,每位市民都可以通过电脑网络或手机微信平台参与,但仅有一次参加机会工作人员通过随机抽样,得到参与网络问卷调查的100人的得分(满分按100分计)数据,统计结果如下表.
组别 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
(1)环保部门规定:问卷得分不低于70分的市民被称为“环保关注者”.请列出![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下,认为是否为“环保关注者”与性别有关?
的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.现在从本次调查的“环保达人”中利用分层抽样的方法随机抽取5名市民参与环保知识问答,再从这5名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“环保达人”又有女“环保达人”的概率.
附表及公式: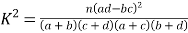 ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
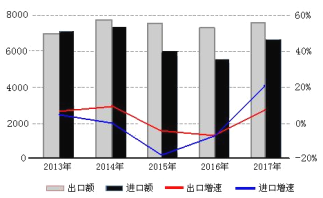
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验中学在教工活动中心举办了一场台球比赛,为了节约时间比赛采取“3局2胜制”.现有甲、乙二人,已知每局甲胜的概率为0.6,乙胜的概率为0.4.求:
(1)这场比赛甲获胜的概率;
(2)这场比赛乙所胜局数的数学期望.
(3)这场比赛在甲获得比赛胜利的条件下,乙有一局获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC⊥BC,O为AB中点,且DC⊥平面ABC,DC∥BE.已知AC=BC=DC=BE=2.
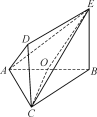
(1)求直线AD与CE所成角;
(2)求二面角O-CE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: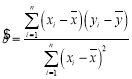 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“
级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“![]() 级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com