
分析 根据求分段函数求定积分,利用奇函数的性质,求得${∫}_{-1}^{3π}$f(x)dx的值.
解答 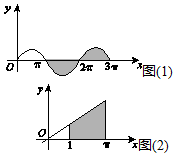 解:由定积分的几何意义知:
解:由定积分的几何意义知:
∵f(x)=x5是奇函数,故${∫}_{-1}^{1}$x5dx=0;
${∫}_{π}^{3π}$sinxdx=-cosx|${\;}_{π}^{3π}$=-(cos3π-cosπ)=0,(如图(1)所示);
${∫}_{1}^{π}$xdx=$\frac{1}{2}$x2|${\;}_{1}^{π}$=$\frac{1}{2}$(1+π)(π-1)=$\frac{1}{2}$(π2-1)(如图(2)所示).
∴${∫}_{-1}^{3π}$f(x)dx=${∫}_{-1}^{1}$x5dx+${∫}_{1}^{π}$xdx+${∫}_{π}^{3π}$sinxdx=0+$\frac{1}{2}$(π2-1)+0=$\frac{1}{2}$(π2-1).
点评 本题考查求分段函数的定积分及定积分的性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 09,14,19,24 | B. | 10,16,22,28 | C. | 16,28,40,52 | D. | 08,12,16,20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1或3 | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a?b)2=a2?b2 | B. | (a?b)?c=a?(b?c) | ||
| C. | (a?b)2=(b?a)2 | D. | c•(a?b)=(c•a)?(c•b)(c>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -log20172016 | B. | -1 | C. | log20172016-1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com