
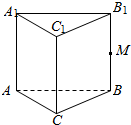
 如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
如图所示,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:分析 利用空间向量的加减法的运算法则和几何意义化简.
解答 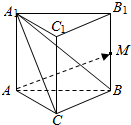 解:(1)$\overrightarrow{CB}$+$\overrightarrow{B{A}_{1}}$=$\overrightarrow{C{A}_{1}}$,
解:(1)$\overrightarrow{CB}$+$\overrightarrow{B{A}_{1}}$=$\overrightarrow{C{A}_{1}}$,
(2)$\overrightarrow{AC}$+$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{A{A}_{1}}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{A{A}_{1}}$=$\overrightarrow{AM}$;
(3)$\overrightarrow{A{A}_{1}}$-$\overrightarrow{AC}$-$\overrightarrow{CB}$=$\overrightarrow{C{A}_{1}}$-$\overrightarrow{CB}$=$\overrightarrow{B{A}_{1}}$.
点评 本题考查了空间向量线性运算及其几何意义,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,3) | C. | (2,4) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{\sqrt{2}}{2}$,+∞) | D. | (0,$\frac{1}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-tanx | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$,$\frac{1}{10}$ | B. | $\frac{3}{10}$,$\frac{1}{5}$ | C. | $\frac{1}{5}$,$\frac{3}{10}$ | D. | $\frac{3}{10}$,$\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com