
分析 不妨设x>y>z,可得$\frac{x-y}{y-z}$=x,$\frac{y-z}{z-x}$=y,$\frac{z-x}{x-y}$=z,由此,即可得出结论.
解答 解:不妨设x>y>z,则,
$\frac{x-y}{y-z}$-$\frac{y-z}{z-x}$=$\frac{{x}^{2}+{y}^{2}+{z}^{2}-(xy+yz+xz)}{(y-z)(z-x)}$>0,
∴$\frac{x-y}{y-z}$>$\frac{y-z}{z-x}$.
同理$\frac{x-y}{y-z}$>$\frac{z-x}{x-y}$,$\frac{y-z}{z-x}$>$\frac{z-x}{x-y}$
∴$\frac{x-y}{y-z}$=x,$\frac{y-z}{z-x}$=y,$\frac{z-x}{x-y}$=z
∵xyz=$\frac{x-y}{y-z}$•$\frac{y-z}{z-x}$•$\frac{z-x}{x-y}$=1,
∴y=-$\frac{1}{1+x}$,z=-$\frac{1+x}{x}$,
∴(x,y,z)=(t,-$\frac{1}{1+t}$,-$\frac{1+t}{t}$)(t≠0,t≠-1)
点评 本题考查大小比较,考查不等式知识的运用,考查学生分析解决问题的能力,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
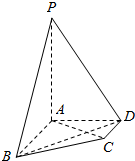 在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.
在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=2,AD=$\sqrt{2}$,CD=1,PA⊥平面ABCD,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ( $\frac{1}{3}$,$\frac{2}{3}$ ) | B. | [$\frac{1}{3}$,$\frac{2}{3}$ ) | C. | ( $\frac{1}{2}$,$\frac{2}{3}$ ) | D. | [$\frac{1}{2}$,1 ) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com