
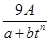 ,其中
,其中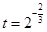 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 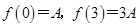 ,运用待定系数法不难求出
,运用待定系数法不难求出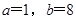 ,进而确定出函数
,进而确定出函数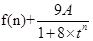 ,其中
,其中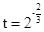 .由
.由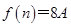 ,运用解方程的方法即可求出
,运用解方程的方法即可求出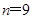 ,问题得解; (2)由前面(1)中已求得
,问题得解; (2)由前面(1)中已求得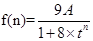 ,可表示出第n年的增长高度为
,可表示出第n年的增长高度为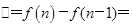
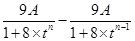 ,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得:
,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得: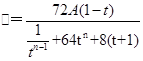 ,观察此式特征能用基本不等式的方法进行求它的最值,即:
,观察此式特征能用基本不等式的方法进行求它的最值,即: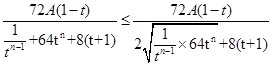 ,成立的条件为 当且仅当
,成立的条件为 当且仅当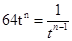 时取等号,即可求出
时取等号,即可求出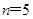 .
. 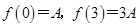 .
.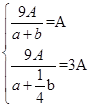 解得
解得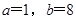 . 4分
. 4分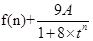 ,其中
,其中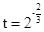 .
.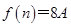 ,得
,得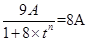 ,解得
,解得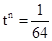 ,
,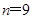 .
. 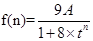 .
.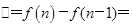
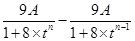 . 9分
. 9分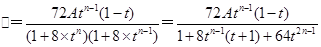
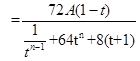 12分
12分 .
.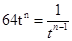 ,即
,即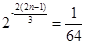 时取等号,此时
时取等号,此时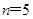 .
.

科目:高中数学 来源:不详 题型:单选题
| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
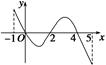
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
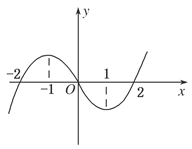
| A.(-∞,-1)∪(0,1) |
| B.(-1,0)∪(1,+∞) |
| C.(-2,-1)∪(1,2) |
| D.(-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
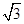 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )| A.1 | B.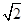 | C.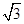 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
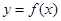 是定义在R上的偶函数,且在[0,+
是定义在R上的偶函数,且在[0,+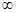 )上单调递增,则满足f(m)<f(1)的实数m的范围是
)上单调递增,则满足f(m)<f(1)的实数m的范围是 A.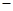 l<m<0 l<m<0 |
| B.0<m<1 |
C.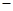 l<m<1 l<m<1 |
D.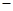 l≤m≤1 l≤m≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com