
【题目】设函数![]()
(1)讨论f(x)的单调性;
(2)求f(x)在区间[﹣2,2]的最大值和最小值.
【答案】(1)f(x)在(﹣∞,﹣2),(﹣1,+∞)上单调递增,在(﹣2,﹣1)上单调递减;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】
(1)求出导函数f′(x),分别解不等式f′(x)>0和f′(x)<0即可得到单调区间;
(2)结合第(1)所求单调性,即可求出最值.
(1)f′(x)=x2+3x+2=(x+1)(x+2),
令f′(x)>0解得x<﹣2或x>﹣1;令f′(x)<0解得﹣2<x<﹣1,
故函数f(x)在(﹣∞,﹣2),(﹣1,+∞)上单调递增,在(﹣2,﹣1)上单调递减;
(2)由(1)可得x,f′(x),f(x)的变化情况,
x | ﹣2 | (﹣2,﹣1) | ﹣1 | (﹣1,2) | 2 |
f′(x) | 0 | ﹣ | 0 | + | |
f(x) |
| 减 | 极小值 | 增 |
|
故函数f(x)在区间[﹣2,2]上的最大值为![]() ,最小值为
,最小值为![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)试确定t的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,又若方程
,又若方程![]() 在
在![]() 上有唯一解,请确定t的取值范围.
上有唯一解,请确定t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上.
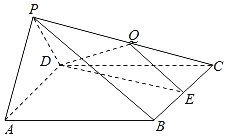
(Ⅰ)求证:AD⊥PB;
(Ⅱ)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(Ⅲ)是否存在Q,使PA∥平面DEQ?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是各项均为非零实数的数列
是各项均为非零实数的数列![]() 的前n项和,给出如下两个命题上:命题p:
的前n项和,给出如下两个命题上:命题p:![]() 是等差数列;命题q:等式
是等差数列;命题q:等式![]() 对任意
对任意![]()
![]() 恒成立,其中k,b是常数.
恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n![]() 和正数M,数列
和正数M,数列![]() 满足条件
满足条件![]() ,试求
,试求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中![]() 浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化
浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化![]() 年除夕18时和初一2时,国家环保部门对8个城市空气中
年除夕18时和初一2时,国家环保部门对8个城市空气中![]() 浓度监测的数据如表
浓度监测的数据如表![]() 单位:微克
单位:微克![]() 立方米
立方米![]() .
.
除夕18时 | 初一2时 | |
北京 | 75 | 647 |
天津 | 66 | 400 |
石家庄 | 89 | 375 |
廊坊 | 102 | 399 |
太原 | 46 | 115 |
上海 | 16 | 17 |
南京 | 35 | 44 |
杭州 | 131 | 39 |
![]() Ⅰ
Ⅰ![]() 求这8个城市除夕18时空气中
求这8个城市除夕18时空气中![]() 浓度的平均值;
浓度的平均值;
![]() Ⅱ
Ⅱ![]() 环保部门发现:除夕18时到初一2时空气中
环保部门发现:除夕18时到初一2时空气中![]() 浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹
浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹![]() 从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
![]() Ⅲ
Ⅲ![]() 记2017年除夕18时和初一2时以上8个城市空气中
记2017年除夕18时和初一2时以上8个城市空气中![]() 浓度的方差分别为
浓度的方差分别为![]() 和
和![]() ,比较
,比较![]() 和
和![]() 的大小关系
的大小关系![]() 只需写出结果
只需写出结果![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是《史记》中记载的一个故事,说的是齐国大将军田忌经常与齐国众公子赛马,孙膑发现田忌的马和其他人的马相差并不远,都分为上、中、下三等.于是孙膑给田忌将军献策:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得了许多赌注.假设田忌的各等级马与某公子的各等级马进行一场比赛,田忌获胜的概率如下表所示:
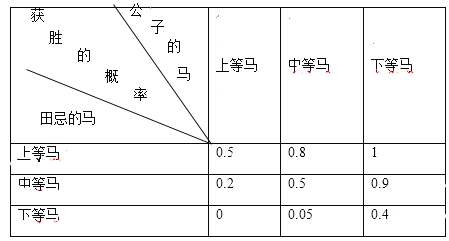
比赛规则规定:一次比赛由三场赛马组成,每场由公子和田忌各出一匹马参赛,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
(1)如果按孙膑的策略比赛一次,求田忌获胜的概率;
(2)如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,
,![]() 为抛物线上在第一象限内一点,
为抛物线上在第一象限内一点,![]() 为原点,
为原点,![]() 面积为
面积为![]() .
.
(1)求抛物线方程;
(2)过![]() 点作两条直线分别交抛物线于异于点
点作两条直线分别交抛物线于异于点![]() 的两点
的两点![]() ,
,![]() ,且两直线斜率之和为
,且两直线斜率之和为![]() ,
,
(i)若![]() 为常数,求证直线
为常数,求证直线![]() 过定点
过定点![]() ;
;
(ii)当![]() 改变时,求(i)中距离
改变时,求(i)中距离![]() 最近的点
最近的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com