
【题目】已知直线y=a分别与直线![]() ,曲线
,曲线![]() 交于点A,B,则线段AB长度的最小值为______.
交于点A,B,则线段AB长度的最小值为______.
【答案】![]()
【解析】
![]() ,设与
,设与![]() 平行的
平行的![]() 的切线的点为
的切线的点为![]() ,则切线斜率为
,则切线斜率为![]() ,
,![]() 切线方程为
切线方程为![]() ,
,![]() 则
则![]() 与
与![]() ,
, ![]() 被直线与切线截得的线段长,就是
被直线与切线截得的线段长,就是![]() 被直线
被直线![]() 和曲线
和曲线![]() 截得线段
截得线段![]() 的最小值,因为
的最小值,因为![]() 取任何值时,
取任何值时,![]() 被两平行线截得的线段长相等,所以令
被两平行线截得的线段长相等,所以令![]() ,可得
,可得![]() ,线段
,线段![]() 的最小值
的最小值![]() ,故答案为
,故答案为![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线方程以及最值问题以及数学的转化与划归思想,属于难题.转化与划归思想解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域,进而顺利解答,希望同学们能够熟练掌握并应用于解题当中. 本题中,将![]() 被直线
被直线![]() 和曲线
和曲线![]() 截得线段
截得线段![]() 的最小值转化为,
的最小值转化为,![]() 被直线
被直线![]() 和曲线
和曲线![]() 截得线段
截得线段![]() 的最小值,是解题的关键.
的最小值,是解题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
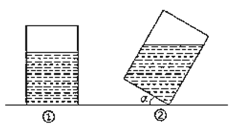
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,侧面
,侧面![]() 为正三角形,侧面
为正三角形,侧面![]() 底面
底面![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,点
,点![]() 为左焦点,过点
为左焦点,过点![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在一点
上是否存在一点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点满足
两点满足![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆![]() 的离心率为
的离心率为![]() ,椭圆上动点
,椭圆上动点![]() 到一个焦点的距离的最小值为
到一个焦点的距离的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)已知过点![]() 的动直线l与椭圆C交于 A,B 两点,试判断以AB为直径的圆是否恒过定点,并说明理由.
的动直线l与椭圆C交于 A,B 两点,试判断以AB为直径的圆是否恒过定点,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
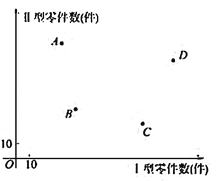
【题目】![]() 四名工人一天中生产零件的情况如图所示,每个点的横、纵坐标分别表示该工人一天中生产
四名工人一天中生产零件的情况如图所示,每个点的横、纵坐标分别表示该工人一天中生产
的Ⅰ型、Ⅱ型零件数,有下列说法:
四个工人中,![]() 的日生产零件总数最大
的日生产零件总数最大
②![]() 日生产零件总数之和小于
日生产零件总数之和小于![]() 日生产零件总数之和
日生产零件总数之和
③![]() 日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和
日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和
④![]() 日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和
日生产Ⅰ型零件总数之和小于Ⅱ型零件总数之和
则正确的说法有__________(写出所有正确说法的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com