
【题目】已知抛物线![]() 的焦点
的焦点![]() 为曲线
为曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 、
、![]() 三个点满足
三个点满足![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
, ![]() ).
).
(1)当![]() 时,若
时,若![]() 在其定义域内为单调函数,求
在其定义域内为单调函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,如果存在,求
恒成立,如果存在,求![]() 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() +
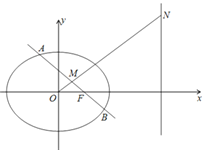
+![]() =1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
=1(a>b>0)的右焦点F(1,0),右准线l:x=4.圆C2:x2+y2=b2.A、B为椭圆上不同的两点,AB中点为M.
(1)求椭圆C1的方程;
(2)若直线AB过F点,直线OM交l于N点,求证:NF⊥AB;
(3)若直线AB与圆C2相切,求原点O到AB中垂线的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P—ABCD的底面ABCD是平行四边形,PA⊥面ABCD,M是AD的中点,N是PC的中点.

(1)求证:MN∥面PAB;
(2)若平面PMC⊥面PAD,求证:CM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来郑州空气污染较为严重,现随机抽取一年(365天)内100天的空气中![]() 指数的监测数据,统计结果如下:
指数的监测数据,统计结果如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时对企业没有造成经济损失;当
内时对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时对企业造成经济损失成直线模型(当
内时对企业造成经济损失成直线模型(当![]() 指数为150时造成的经济损失为500元,当
指数为150时造成的经济损失为500元,当![]() 指数为200时,造成的经济损失为700元);当
指数为200时,造成的经济损失为700元);当![]() 指数大于300时造成的经济损失为2000元.
指数大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于500元且不超过900元的概率;
大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面列联表,并判断是否有![]() 的把握认为郑州市本年度空气重度污染与供暖有关?
的把握认为郑州市本年度空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
![]() ,其中
,其中![]() .
.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距640米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为![]() 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为![]() 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,设需要新建![]() 个桥墩,记余下工程的费用为
个桥墩,记余下工程的费用为![]() 万元.
万元.
(1)试写出![]() 关于
关于![]() 的函数关系式;(注意:
的函数关系式;(注意:![]() )
)
(2)需新建多少个桥墩才能使![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,且a1=1,S3+S4=S5.
(1)求数列{an}的通项公式;
(2)令bn=(-1)n-1an,求数列{bn}的前2n项和T2n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com