函数f(x)=loga(x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,Q(x-2a,-y)是函数y=g(x)图象上的点.
(1)写出函数y=g(x)的解析式.?
(2)当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
【答案】
分析:(1)由题设条件,点P(x,y)是函数y=f(x)图象上的点时,Q(x-2a,-y)是函数y=g(x)图象上的点.求解函数y=g(x)的解析式可用代入法.
(2)由x∈[a+2,a+3],及两对数函数有意义可以得到0<a<1,由此可以得到对数函数是减函数,由单调性将恒等式转化为一元二次不等式
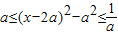
,构造函数h(x)=(x-2a)
2-a
2,求出h(x)在定义域[a+2,a+3]上的最大值与最小值,再一次将问题转化为
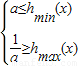
,即得参数a的不等式组,解之求得参数的范围.
解答:解:(1)设P(x
,y
)是y=f(x)图象上点,令Q(x,y),则
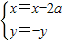
,
∴
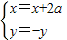
∴-y=log
a(x+2a-3a),∴y=log
a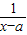
(x>a)
(2)由对数函数的定义得
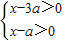
∴x>3a
∵f(x)与g(x)在[a+2,a+3]上有意义.
∴3a<a+2
∴0<a<1(6分)
∵|f(x)-g(x)|≤1恒成立⇒|log
a(x-3a)(x-a)|≤1恒成立.
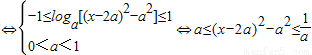
对x∈[a+2,a+3]上恒成立,令h(x)=(x-2a)
2-a
2其对称轴x=2a,2a<2,2<a+2
∴当x∈[a+2,a+3]
h
min(x)=h(a+2),h
max=h(a+3)
∴原问题等价
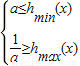
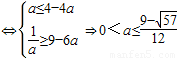 点评:
点评:本题考点是指数函数综合题,考查根据指数函数的相关性质求参数范围,解决本题关键是根据单调性将问题转化关于参数的方程或不等式组,恒成立问题求参数其规律基本上都是将问题如本题一样转化,请认真体会本解法中问题转化的依据与转化的方式.

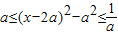 ,构造函数h(x)=(x-2a)2-a2,求出h(x)在定义域[a+2,a+3]上的最大值与最小值,再一次将问题转化为
,构造函数h(x)=(x-2a)2-a2,求出h(x)在定义域[a+2,a+3]上的最大值与最小值,再一次将问题转化为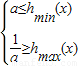 ,即得参数a的不等式组,解之求得参数的范围.
,即得参数a的不等式组,解之求得参数的范围.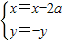 ,
,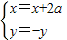 ∴-y=loga(x+2a-3a),∴y=loga
∴-y=loga(x+2a-3a),∴y=loga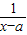 (x>a)
(x>a)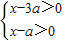
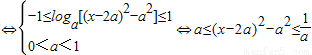
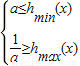
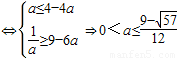


 快乐5加2金卷系列答案
快乐5加2金卷系列答案