
����Ŀ���йز���Ҫ�˽����H1N1����Ԥ��֪ʶ��ѧУ���ռ������������һ����10������ʾ�������ѧУ���ʾ����顣ij��ѧA��B��������������ȡ5��ѧ�������ʾ����飬A��5��ѧ���÷ֱַ�Ϊ��5, 8, 9�� 9�� 9��B��5��ѧ���ĵ÷ֱַ�Ϊ��6, 7, 8, 9, 10��
��1���������A��B���������ĸ�����ʾ��÷�Ҫ�ȶ�Щ��
��2�������B��5��ѧ���ĵ÷ֿ���һ�����壬���ü���������������г�ȡ����Ϊ2��������������ƽ����������ƽ����֮��ľ���ֵ��С��1�ĸ��ʡ�
���𰸡���1������������2��![]() .
.
����������������1�������ֵ��һ���������ѡ���С�ģ���2����ȷ�����¼�������ȷ������ƽ����������ƽ����֮��ľ���ֵ��С��1���¼����������ݹŵ�����ʹ�ʽ����.
��⣺
����![]() ���
���![]() ��ѧ����ƽ���÷�Ϊ
��ѧ����ƽ���÷�Ϊ![]()
![]() ��
��![]()
����![]()
![]() ���
���![]() ��ѧ����ƽ���÷�Ϊ
��ѧ����ƽ���÷�Ϊ![]()
![]() ��
��![]()
����![]()
��![]()
![]() ��
�� ![]() ��
��
��![]() ��Ԥ��֪ʶ���ʾ��÷�Ҫ�ȶ�һЩ��
��Ԥ��֪ʶ���ʾ��÷�Ҫ�ȶ�һЩ��
����![]() ��
��![]() ��ͬѧ����ѡ
��ͬѧ����ѡ![]() ��ͬѧ�ķ�������
��ͬѧ�ķ�������![]() �֣�
�֣�
��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ƽ��������������
��ƽ��������������
���������Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1������![]() �ĵ���������
�ĵ���������
��2����![]() ʱ���жϺ���
ʱ���жϺ���![]() ������
������![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() ������
������![]() .
.
��1����![]() ������
������![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2����![]() ��
�� ![]() ����
����![]() ��ֵ��
��ֵ��
��3��������![]() ������
������![]() ���ǵ�������������������
���ǵ�������������������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��2��3��4��5��6������ֲ��ظ�����λ��������1�����������ˣ�2��4��6����ż���У�����ֻ������ż�����ڣ�����������λ���ĸ���Ϊ��������
A.432
B.288
C.216
D.144
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ӵ�ij��Ա���һ�Σ�����7~10���ĸ��������ʾ��
����� | 10�� | 9�� | 8�� | 7�� |
���� | 0.32 | 0.28 | 0.18 | 0.12 |
��������Ա���һ�� ��:
��1������9����10���ĸ��ʣ�
��2����������8���ĸ��ʣ���3�����в���8���ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��(5![]() cos x��cos x)��b��(sin x,2cos x)���躯��f(x)��a��b��|b|2��
cos x��cos x)��b��(sin x,2cos x)���躯��f(x)��a��b��|b|2��![]() .
.
(1) ����f (x)����С�����ںͶԳ�������
(2) ��![]() ʱ������f(x)��ֵ��
ʱ������f(x)��ֵ��
(3) �ú���y��f (x)��ͼ�����![]() ��ͼ�������ı任�õ�?
��ͼ�������ı任�õ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У�����ԲM�� ![]() ��a��b��0���ҽ����ֱ��x+y��
��a��b��0���ҽ����ֱ��x+y�� ![]() =0��M��A��B���㣬PΪAB���е㣬��OP��б��Ϊ
=0��M��A��B���㣬PΪAB���е㣬��OP��б��Ϊ ![]() ��
��
��1����M�ķ���
��2��C��DΪM�ϵ����㣬���ı���ACBD�ĶԽ���CD��AB�����ı���ACBD��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
�У� ![]() ���߶�
���߶�![]() ���˶��Ҳ���
���˶��Ҳ���![]() ��
�� ![]() �غϣ��������н��ۣ�
�غϣ��������н��ۣ�
��![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
�������![]() �Ĵ�С��
�Ĵ�С��![]() ����˶����仯��
����˶����仯��
������![]() ��ƽ��
��ƽ��![]() �ϵ�ͶӰ���������ƽ��
�ϵ�ͶӰ���������ƽ��![]() �ϵ�ͶӰ�����֮����
�ϵ�ͶӰ�����֮����![]() ����˶����仯��
����˶����仯��
������ȷ���ǣ� ��
A. �٢ۢ� B. �٢�
C. �٢ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߳�Ϊ1��������AA1O1O�������ڲ�����OO1��תһ���γ�Բ������ͼ�� ��AC ��Ϊ ![]() ����A1B1 ��Ϊ
����A1B1 ��Ϊ ![]() ������B1��C��ƽ��AA1O1O��ͬ�࣮
������B1��C��ƽ��AA1O1O��ͬ�࣮ 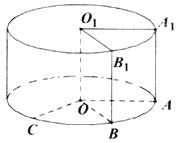
��1����Բ���������������
��2��������ֱ��O1B1��OC���ɵĽǵĴ�С��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com