
【题目】已知动点![]() 到定点
到定点![]() 的距离之和为4.
的距离之和为4.
(1)求动点![]() 的轨迹方程
的轨迹方程![]()
(2)若轨迹![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 求
求![]() 的值.
的值.
(3)若点![]() 与点
与点![]() 在轨迹
在轨迹![]() 上,且点
上,且点![]() 在第一象限,点
在第一象限,点![]() 在第二象限,点
在第二象限,点![]() 与点
与点![]() 关于原点对称,求证:当
关于原点对称,求证:当![]() 时,三角形
时,三角形![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)定值
;(3)定值![]() ,见解析
,见解析
【解析】
(1)求得椭圆的![]() ,即可求动点
,即可求动点![]() 的轨迹方程
的轨迹方程![]()
(2)将直线![]() 代入椭圆方程
代入椭圆方程![]() ,可得
,可得![]() 的方程,运用韦达定理和判别式大于0,由弦长公式,解方程即可得到所求值;
的方程,运用韦达定理和判别式大于0,由弦长公式,解方程即可得到所求值;
(3)求出直线AB的方程,运用点到直线的距离公式求得P到直线AB的距离,弦长AB,运用三角形的面积公式可得![]() ,再由A,P满足椭圆方程,结合条件
,再由A,P满足椭圆方程,结合条件![]() ,计算即可得到三角形
,计算即可得到三角形![]() 的面积为定值.
的面积为定值.
(1)动点Q到两定点![]() 、
、![]() 的距离和为4,满足椭圆的定义,且
的距离和为4,满足椭圆的定义,且![]()
![]()
![]() ,
,![]() 动点
动点![]() 的轨迹方程
的轨迹方程![]() :
:![]()
(2)将直线![]() 代入椭圆方程
代入椭圆方程![]() ,可得
,可得![]() ,
,![]() ,解得
,解得![]() ,
,
设![]()
![]()
则![]()
![]()
即有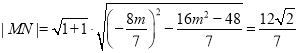 ,
,
解得![]() ,满足
,满足![]()
(3)证明:直线AB的方程为![]() ,即为
,即为![]() ,
,
可得![]() 到直线AB的距离为
到直线AB的距离为 ,
,![]() ,
,
则![]() ═
═![]() ,
,
由![]() ,得
,得![]()
![]() 因为
因为![]()
![]()
可得![]()
![]()
则![]()
由![]() ,可得
,可得![]()
![]()
即有![]()
故当![]() 时,三角形
时,三角形![]() 的面积为定值
的面积为定值![]()


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
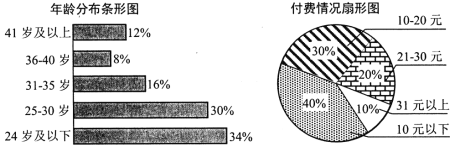
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
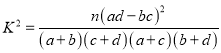 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=BC=4,BB1=2![]() ,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
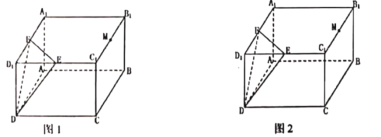
(1)在图1中,画出这个几何图形,并求这个几何图形的面积(不必说明画法与理由)
(2)在图2中,求证:D1B⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由非负整数组成的无穷数列,对每一个正整数
是由非负整数组成的无穷数列,对每一个正整数![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() 的最小值记为
的最小值记为![]() ,记
,记![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)证明:“数列![]() 单调递增”是“
单调递增”是“![]() ”的充要条件;
”的充要条件;
(3)若![]() 对任意
对任意![]() 恒成立,证明:数列
恒成立,证明:数列![]() 的通项公式为
的通项公式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谈祥柏先生是我国著名的数学科普作家,他写的《数学百草园》、《好玩的数学》、《故事中的数学》等书,题材广泛、妙趣横生,深受广大读者喜爱.下面我们一起来看《好玩的数学》中谈老的一篇文章《五分钟内挑出埃及分数》:文章首先告诉我们,古埃及人喜欢使用分子为1的分数(称为埃及分数).如用两个埃及分数![]() 与
与![]() 的和表示
的和表示![]() 等.从
等.从![]() 这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
这100个埃及分数中挑出不同的3个,使得它们的和为1,这三个分数是________.(按照从大到小的顺序排列)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com