
 ,a1+a2+…+an=n2an,则数列{an}的前60项和为________.
,a1+a2+…+an=n2an,则数列{an}的前60项和为________.
 =
=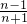 .用累乘的方法算出当n≥2时,an=
.用累乘的方法算出当n≥2时,an= ,且n=1时也符合条件.由此可得{an}的前n项和为和为Sn的表达式,从而得到{an}的前60项和的值.
,且n=1时也符合条件.由此可得{an}的前n项和为和为Sn的表达式,从而得到{an}的前60项和的值. =
=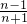 ,
,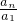 =
= ×
× ×
× ×…×
×…× =
= ×
× ×…×
×…×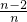 ×
×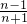 =
=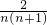
 ,可得an=
,可得an=
 对任意n∈N+成立,
对任意n∈N+成立, =
= -
- ,
, )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+( -
- )=1-
)=1- =
= .
.



 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
| a | 2 n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| m |
查看答案和解析>>
科目:高中数学 来源:2013年福建省三明市高三质量检查数学试卷(解析版) 题型:选择题
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )

查看答案和解析>>
科目:高中数学 来源:2012年福建省三明市普通高中毕业班质量检查数学试卷(理科)(解析版) 题型:选择题
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com