【题目】在平面直角坐标系
中，
，
，动点
满足：直线
与直线
的斜率之积恒为
，记动点的轨迹为曲线
.
（1）求曲线的方程；
（2）若点位于第一象限，过点
，
分别作直线
，直线
，直线
，
交于点
.
①若点的横坐标为-1，求点的坐标；
②直线与曲线交于点
，且
，求
的取值范围.
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：高中数学 来源： 题型：
【题目】在半径为
的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是________
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点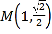
在椭圆上E：
（
），点
为平面上一点，O为坐标原点．
（1）当
取最小值时，求椭圆E的方程；
（2）对（1）中的椭圆E，P为其上一点，若过点
的直线l与椭圆E相交于不同的两点S和T，且满足
（
），求实数t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为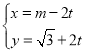
（
，
为参数），曲线
的参数方程为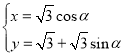
（
为参数），直线与曲线交于
，
两点.
（1）以坐标原点为极点，
轴正半轴为极轴建立极坐标系，求曲线的极坐标方程；
（2）若
，点
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为进一步优化教育质量平台，更好的服务全体师生，七天网络从甲、乙两所学校各随机抽取100名考生的某次“四省八校”数学考试成绩进行分析，分别绘制的频率分布直方图如图所示.
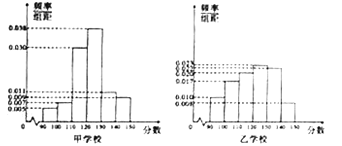
为了更好的测评各个学校数学学科的教学质量，该公司依据每一位考生的数学测试分数将其划分为“
，
，
”三个不同的等级，并按照不同的等级，设置相应的对学校数学学科教学质量贡献的积分，如下表所示.
测试分数 | 分数对应的等级 | 贡献的积分 |
|
| 1分 |
|
| 2分 |
|
| 3分 |
（1）用样本的频率分布估计总体的频率分布，若将甲学校考生的数学测试等级划分为“等”和“非等”两种，利用分层抽样抽取10名考生，再从这10人随机抽取3人，求3人中至少1人数学测试为“等”的概率；
（2）视频率分布直方图中的频率为概率，用样本估计总体，若从乙学校全体考生中随机抽取3人，记3人中数学测试等级为“等”的人数为
，求的分布列和数学期望
；
（3）根据考生的数学测试分数对学校数学学科教学质量贡献的积分规则，分别记甲乙两所学校数学学科质量的人均积分为
和
，用样本估计总体，求和的估计值，并以此分析，你认为哪所学校本次数学教学质量更加出色？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，定义
为两点
、
的“切比雪夫距离”，又设点
及
上任意一点
，称
的最小值为点到直线的“切比雪夫距离”，记作
，给出四个命题，正确的是________.
①对任意三点
、
、
，都有
；
② 到原点的“切比雪夫距离”等于
的点的轨迹是正方形；
③ 已知点
和直线
，则
；
④ 定点
、
，动点
满足
，则点的轨迹与直线
（
为常数）有且仅有
个公共点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
、
、
、
是同一平面上不共线的四点，若存在一组正实数
、
、
，使得
，则三个角
、
、
（ ）
A. 都是钝角B. 至少有两个钝角
C. 恰有两个钝角D. 至多有两个钝角
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合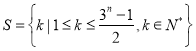
（
，且
），若存在非空集合
，使得
，且
，并任意
，都有
，则称集合S具有性质P，
称为集合S的P子集.
（1）当
时，试说明集合S具有性质P，并写出相应的P子集
；
（2）若集合S具有性质P，集合T是集合S的一个P子集，设
，求证：任意
，
，都有
；
（3）求证：对任意正整数，集合S具有性质P.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
