
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:不详 题型:解答题
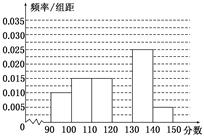
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.0.35 | B.0.25 | C.0.20 | D.0.15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
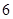 个面的中心,甲从这
个面的中心,甲从这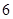 个点中任意选两个点连成直线,乙也从这
个点中任意选两个点连成直线,乙也从这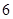 个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )
个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( )A.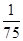 | B.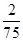 | C.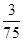 | D.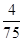 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
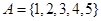 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组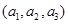 ,规定
,规定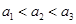
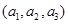 的“项标距离”为
的“项标距离”为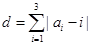 ,(其中
,(其中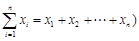 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”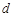 为偶数的概率;
为偶数的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
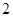 个红球和
个红球和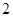 个黒球的口袋内任取
个黒球的口袋内任取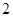 个球,互斥而不对立的两个事件是:
个球,互斥而不对立的两个事件是:| A.至少有一个黒球与都是黒球 | B.至少有一个红球与都是红球 |
C.至少有一个黒球与至少有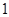 个红球 个红球 | D.恰有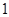 个黒球与恰有 个黒球与恰有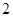 个黒球 个黒球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com