考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)求出函数的导数,令导数大于0,小于0,分别解出不等式即可;
(2)切线的斜率即为函数在切点处的导数,让f′(x
0)=
≤
恒成立即可,再由不等式恒成立时所取的条件得到实数a范围,即得实数a的最小值.
解答:
解:由f(x)=lnx+
(a>0),得到f′(x)=
(1)令f′(x)>0,得到x-a>0,故函数f(x)的单调递增区间为(a,+∞),
令f′(x)<0,得到x-a<0,故函数f(x)的单调递减区间为(0,a),
故函数f(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(2)由于f′(x
0)=
,且以y=f(x)(x∈(0,3])图象上任意一点P(x
0,y
0)为切点的切线的斜率k≤
恒成立
则f′(x
0)=
≤
在(0,3]上恒成立,即a≥x
0-
x02在(0,3]上恒成立,
令g(x)=x
0-
x02(0<x≤3),可知g(x)
max=g(1)=
,
∴a≥
,
故实数a的最小值为
.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.同时考查利用导数求曲线上过某点切线方程的斜率,不等式恒成立时所取的条件.



 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案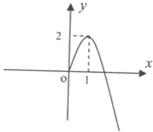 已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.
已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.