Question

8．设函数f（x）=|sinx|的图象与直线y=kx（k＞0）有且仅有三个公共点，这三个公共点横坐标的最大值为α，则α等于（　　）

• A． tanα
• B． -cosα
• C． sinα
• D． π

Answer 1

分析 根据题意，画出图象，然后根据切线斜率的定义以及斜率公式，求得-$\frac{sinα}{α}$=-cosα，由此可得α的值．

解答 解：如图所示：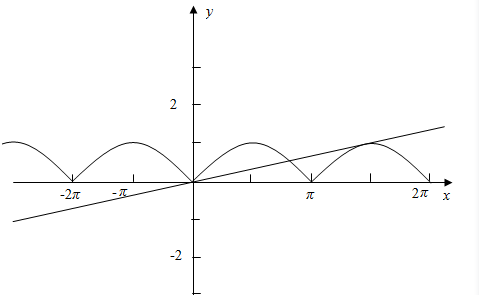

∵函数f（x）=|sinx|的图象与y=kx仅有三个公共点，
这三个公共点横坐标的最
大值为α，
则α∈（π，$\frac{3π}{2}$）．
∵直线y=kx与 y=-sinx
相切，
∴k=-$\frac{-sinα}{α}$，同时，
由 y'=-cosx，
∴k=-cosα．
因此，-$\frac{sinα}{α}$=-cosα，
∴α=tanα，
故选：A．

点评 本题重点考查了三角函数图象与性质、三角函数图象变换等知识，属于中档题．解题关键是数形结合思想在解题中的应用，属于中档题．