
分析 (Ⅰ)若进行n局比赛,则甲获胜的概率为$(\frac{1}{2})^{n}$;若进行n+1局比赛,则最后一局比赛甲获胜,且前n局比赛中甲负一局;若进行n+2局比赛,则最后一局比赛甲获胜,且前n局比赛中甲负两局.由此能求出甲获胜的概率.
(Ⅱ)用A表示甲羸得比赛的事件,Ak表示第k局甲获胜,Bk表示第k局乙获胜,比赛总局数X的可能取值为2,3,4,5,分别求出相应的概率,由此能求出X的分布列与期望.
解答 解:(Ⅰ)若进行n局比赛,则甲获胜的概率为$(\frac{1}{2})^{n}$,
若进行n+1局比赛,则最后一局比赛甲获胜,且前n局比赛中甲负一局,概率为${C}_{n}^{1}(\frac{1}{2})^{n+1}$,
若进行n+2局比赛,则最后一局比赛甲获胜,且前n局比赛中甲负两局,概率为${C}_{n}^{2}(\frac{1}{2})^{n+2}$,
∴甲获胜的概率P=$(\frac{1}{2})^{n}+{C}_{n}^{1}(\frac{1}{2})^{n+1}+{C}_{n}^{2}(\frac{1}{2})^{n+2}$.
(Ⅱ)用A表示甲羸得比赛的事件,Ak表示第k局甲获胜,Bk表示第k局乙获胜,
比赛总局数X的可能取值为2,3,4,5,
P(X=2)=P(A1A2)+P(B1B2)=$\frac{1}{2}×\frac{1}{2}+\frac{1}{2}×\frac{1}{2}$=$\frac{1}{2}$,
P(X=3)=P(A1B2B3)+P(B1A2A3)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}+\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}+\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{8}$,
P(X=5)=P(A1B2A3B4A2)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)
=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}+\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$+$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}+\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{8}$,
∴X的分布列为:
| X | 2 | 3 | 4 | 5 |
| P | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{8}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件乘法概率公式和互斥事件概率加法公式的合理运用.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
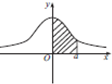 如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )
如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 8 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
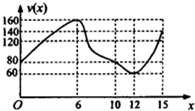 一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )
一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )| A. | 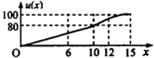 | B. | 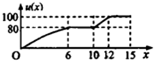 | ||
| C. | 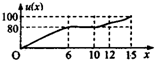 | D. | 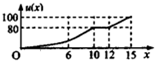 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com