
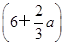 元时,分公司一年的利润L最大,最大值Q(a)=4
元时,分公司一年的利润L最大,最大值Q(a)=4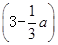 3(万元).
3(万元).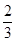 a或x=12(不合题意,舍去).
a或x=12(不合题意,舍去).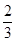 a≤
a≤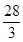 .
.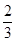 a两侧,L′的值由正变负.
a两侧,L′的值由正变负.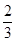 a<9,
a<9,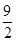 时,
时,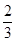 a≤
a≤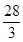 ,
,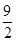 ≤a≤5时,
≤a≤5时,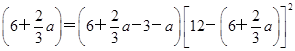 2
2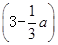 3,所以Q(a)=
3,所以Q(a)=
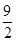 ,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若
,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若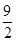 ≤a≤5,则当每件售价为
≤a≤5,则当每件售价为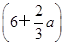 元时,分公司一年的利润L最大,最大值Q(a)=4
元时,分公司一年的利润L最大,最大值Q(a)=4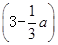 3(万元)
3(万元)

 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )A.(-∞,-1)∪(- ,0) ,0) | B.{-1,- } } |
C.(-1,- ) ) | D.(-∞,-1)∪[- ,0) ,0) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.
log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).| A.x1+x2>0,y1+y2>0 |
| B.x1+x2<0,y1+y2>0 |
| C.x1+x2>0,y1+y2<0 |
| D.x1+x2<0,y1+y2<0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则f(x)可以是( ).
,则f(x)可以是( ).A.f(x)=2x- | B.f(x)=-x2+x- |
| C.f(x)=1-10x | D.f(x)=ln (8x-2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费C(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是C(x)=
,为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费C(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是C(x)= (x>0).记该企业安装这种太阳能供电设备的费用与该企业15年共将消耗的电费之和为F(x)(万元),则F(40)等于( )
(x>0).记该企业安装这种太阳能供电设备的费用与该企业15年共将消耗的电费之和为F(x)(万元),则F(40)等于( )| A.80 | B.60 | C. | D.40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com