
【题目】已知函数f(x)=ex(其中e为自然对数的底数),g(x)= ![]() x+m(m,n∈R).
x+m(m,n∈R).
(1)若T(x)=f(x)g(x),m=1﹣ ![]() ,求T(x)在[0,1]上的最大值;
,求T(x)在[0,1]上的最大值;
(2)若m=﹣ ![]() ,n∈N* , 求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<
,n∈N* , 求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2< ![]() ].
].
【答案】
(1)解:T(x)=f(x)g(x)
=ex( ![]() x+m)=ex(
x+m)=ex( ![]() x+1﹣
x+1﹣ ![]() );
);
故T′(x)=ex( ![]() x+1);
x+1);
则当n≥﹣2时,T′(x)≥0;
故T(x)在[0,1]上的最大值为T(1)=e;
当n<﹣2时,x∈[0,﹣ ![]() )时,T′(x)>0;x∈(﹣
)时,T′(x)>0;x∈(﹣ ![]() ,1]时,T′(x)<0;
,1]时,T′(x)<0;
T(x)在[0,1]上的最大值为T(﹣ ![]() )=﹣
)=﹣ ![]()
(2)解:由题意,f(x)=ex,g(x)= ![]() x﹣
x﹣ ![]() ;
;
故f(x)的图象恒在g(x)图象上方可化为
F(x)=f(x)﹣g(x)=ex﹣ ![]() x+
x+ ![]() >0恒成立;F′(x)=ex﹣
>0恒成立;F′(x)=ex﹣ ![]() ;
;
故F(x)在(﹣∞,ln ![]() )上是减函数,在(ln
)上是减函数,在(ln ![]() ,+∞)上是增函数;
,+∞)上是增函数;
故可化为F(ln ![]() )>0;即
)>0;即 ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() >0;
>0;
令G(n)= ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() ;故G′(n)=﹣
;故G′(n)=﹣ ![]() (ln
(ln ![]() +1)<0;
+1)<0;
故G(n)= ![]() (1﹣ln
(1﹣ln ![]() )+
)+ ![]() 是[1,+∞)上的减函数,
是[1,+∞)上的减函数,
而G(2e2)=﹣e2+ ![]() >0;G(14)=7(1﹣ln7)+
>0;G(14)=7(1﹣ln7)+ ![]() >0;
>0;
G(15)=7.5(1﹣ln7.5)+ ![]() <0;故最大正整数n为14
<0;故最大正整数n为14
【解析】(1)T(x)=f(x)g(x)=ex( ![]() x+m)=ex(
x+m)=ex( ![]() x+1﹣
x+1﹣ ![]() );求导T′(x)=ex(
);求导T′(x)=ex( ![]() x+1);从而确定函数的最大值;(2)由题意,f(x)=ex,g(x)=
x+1);从而确定函数的最大值;(2)由题意,f(x)=ex,g(x)= ![]() x﹣
x﹣ ![]() ;故f(x)的图象恒在g(x)图象上方可化为F(x)=f(x)﹣g(x)=ex﹣
;故f(x)的图象恒在g(x)图象上方可化为F(x)=f(x)﹣g(x)=ex﹣ ![]() x+
x+ ![]() >0恒成立;从而化为最值问题.
>0恒成立;从而化为最值问题.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
……
问:(1)此表第n行的第一个数与最后一个数分别是多少?
(2)此表第n行的各个数之和是多少?
(3)2012是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aex﹣xlnx,其中a∈R,e是自然对数的底数.
(Ⅰ)若f(x)是(0,+∞)上的增函数,求a的取值范围;
(Ⅱ)若 ![]() ,证明:f(x)>0.
,证明:f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣1,+∞)上的单调函数f(x),对于任意的x∈(﹣1,+∞),f[f(x)﹣xex]=0恒成立,则方程f(x)﹣f′(x)=x的解所在的区间是( )
A.(﹣1,﹣ ![]() )
)
B.(0, ![]() )
)
C.(﹣ ![]() ,0)
,0)
D.( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 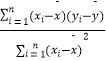 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=sin(2x+φ)+b,对任意实数x都有f(x+ ![]() )=f(﹣x),f(
)=f(﹣x),f( ![]() )=﹣1,则实数b的值为( )
)=﹣1,则实数b的值为( )
A.﹣2或0
B.0或1
C.±1
D.±2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数列{an},如果k∈N*及λ1 , λ2 , …,λk∈R,使an+k=λ1an+k﹣1+λ2an+k﹣2+…+λkan成立,其中n∈N* , 则称{an}为k阶递归数列.给出下列三个结论: ①若{an}是等比数列,则{an}为1阶递归数列;
②若{an}是等差数列,则{an}为2阶递归数列;
③若数列{an}的通项公式为 ![]() ,则{an}为3阶递归数列.
,则{an}为3阶递归数列.
其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=an+n2﹣1,数列{bn}满足3nbn+1=(n+1)an+1﹣nan , 且b1=3,a1=3.
(1)求数列{ an}和{bn}的通项an , bn;
(2)设Tn为数列{bn}的前n项和,求Tn , 并求满足Tn<7时n的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com