
ЁОЬтФПЁПФГЖљЭЏНкдкЁАСљвЛЁБЖљЭЏНкЭЦГіСЫвЛЯюШЄЮЖЛюЖЏЃЎВЮМгЛюЖЏЕФЖљЭЏашзЊЖЏШчЭМЫљЪОЕФзЊХЬСНДЮЃЌУПДЮзЊЖЏКѓЃЌД§зЊХЬЭЃжЙзЊЖЏЪБЃЌМЧТМжИеыЫљжИЧјгђжаЕФЪ§ЃЎМЧСНДЮМЧТМЕФЪ§ЗжБ№ЮЊxЃЌyЃЎНБРјЙцдђШчЯТЃК
ЂйШєxyЁм3ЃЌдђНБРјЭцОпвЛИіЃЛ
ЂкШєxyЁн8ЃЌдђНБРјЫЎБвЛИіЃЛ
ЂлЦфгрЧщПіНБРјвћСЯвЛЦПЃЎ
МйЩшзЊХЬжЪЕиОљдШЃЌЫФИіЧјгђЛЎЗжОљдШЃЌаЁССзМБИВЮМгДЫЯюЛюЖЏЃЎ
ЃЈ1ЃЉЧѓаЁССЛёЕУЭцОпЕФИХТЪЃЛ
ЃЈ2ЃЉЧыБШНЯаЁССЛёЕУЫЎБгыЛёЕУвћСЯЕФИХТЪЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКСНДЮМЧТМЕФЪ§ЮЊЃЈ1ЃЌ2ЃЉЃЌЃЈ1ЃЌ3ЃЉЃЌЃЈ1ЃЌ4ЃЉЃЌЃЈ2ЃЌ3ЃЉЃЌЃЈ2ЃЌ4ЃЉЃЌЃЈ3ЃЌ4ЃЉЃЌЃЈ2ЃЌ1ЃЉЃЌЃЈ3ЃЌ1ЃЉЃЌЃЈ4ЃЌ1ЃЉЃЌЃЈ3ЃЌ2ЃЉЃЌЃЈ4ЃЌ2ЃЉЃЌЃЈ4ЃЌ3ЃЉЃЌЙВ12ИіЃЌ
ТњзуxyЁм3ЃЌгаЃЈ1ЃЌ2ЃЉЃЌЃЈ1ЃЌ3ЃЉЃЌЃЈ2ЃЌ1ЃЉЃЌЃЈ3ЃЌ1ЃЉЃЌЙВ4ИіЃЌ
ЁраЁССЛёЕУЭцОпЕФИХТЪЮЊ ![]() =
= ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ
НтЃКТњзуxyЁн8ЃЌЃЈ2ЃЌ4ЃЉЃЌЃЈ3ЃЌ4ЃЉЃЌЃЈ4ЃЌ2ЃЉЃЌЃЈ4ЃЌ3ЃЉЃЌЙВ4ИіЃЌЁраЁССЛёЕУЫЎБЕФИХТЪЮЊ ![]() =
= ![]() ЃЛ
ЃЛ
аЁССЛёЕУвћСЯЕФИХТЪЮЊ1Љ ![]() Љ
Љ ![]() =
= ![]() ЃЌ
ЃЌ
ЁраЁССЛёЕУЫЎБгыЛёЕУвћСЯЕФИХТЪЯрЕШ
ЁОНтЮіЁПЃЈ1ЃЉШЗЖЈЛљБОЪТМўЕФИХТЪЃЌРћгУЙХЕфИХаЭЕФИХТЪЙЋЪНЧѓаЁССЛёЕУЭцОпЕФИХТЪЃЛЃЈ2ЃЉЧѓГіаЁССЛёЕУЫЎБгыЛёЕУвћСЯЕФИХТЪЃЌМДПЩЕУГіНсТлЃЎЃЛБОЬтПМВщИХТЪЕФМЦЫуЃЌПМВщЙХЕфИХаЭЃЌШЗЖЈЛљБОЪТМўЕФИіЪ§ЪЧЙиМќЃЎ
ЁОПМЕуОЋЮіЁПРћгУМИКЮИХаЭЖдЬтФПНјааХаЖЯМДПЩЕУЕНД№АИЃЌашвЊЪьжЊМИКЮИХаЭЕФЬиЕуЃК1ЃЉЪдбщжаЫљгаПЩФмГіЯжЕФНсЙћЃЈЛљБОЪТМўЃЉгаЮоЯоЖрИіЃЛ2ЃЉУПИіЛљБОЪТМўГіЯжЕФПЩФмадЯрЕШЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЖЅЕуЮЊAЃЌгвНЙЕуЮЊFЃЌЙ§ЕуFЕФжБЯпНЛЭждВгкBЃЌCСНЕуЃЎ
ЕФзѓЖЅЕуЮЊAЃЌгвНЙЕуЮЊFЃЌЙ§ЕуFЕФжБЯпНЛЭждВгкBЃЌCСНЕуЃЎ
(1)ЧѓИУЭждВЕФРыаФТЪЃЛ
(2)ЩшжБЯпABКЭACЗжБ№гыжБЯпxЃН4НЛгкЕуMЃЌNЃЌЮЪЃКxжсЩЯЪЧЗёДцдкЖЈЕуPЪЙЕУMPЁЭNPЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуA(0ЃЌЃ2)ЃЌЭждВEЃК ![]() (a>b>0)ЕФРыаФТЪЮЊ
(a>b>0)ЕФРыаФТЪЮЊ![]() ЃЌFЪЧЭждВEЕФгвНЙЕуЃЌжБЯпAFЕФаБТЪЮЊ
ЃЌFЪЧЭждВEЕФгвНЙЕуЃЌжБЯпAFЕФаБТЪЮЊ![]() ЃЌOЮЊзјБъдЕу.
ЃЌOЮЊзјБъдЕу.
(1)ЧѓEЕФЗНГЬЃЛ
(2)ЩшЙ§ЕуAЕФЖЏжБЯпlгыEЯрНЛгкPЃЌQСНЕу.ЕБЁїOPQЕФУцЛ§зюДѓЪБЃЌЧѓlЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЫФБпаЮ
жаЃЌЫФБпаЮ![]() ЪЧжБНЧЬнаЮЃЌ
ЪЧжБНЧЬнаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ

ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЖўУцНЧ![]() ЕФгрЯвжЕЮЊ
ЕФгрЯвжЕЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕЃЎ
ЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖVЉABCжаЃЌЦНУцVABЁЭЦНУцABCЃЌЁїVABЮЊЕШБпШ§НЧаЮЃЌACЁЭBCЧвAC=BC=![]() ЃЌOЃЌMЗжБ№ЮЊABЃЌVAЕФжаЕуЃЎ
ЃЌOЃЌMЗжБ№ЮЊABЃЌVAЕФжаЕуЃЎ
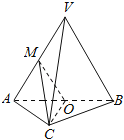
ЃЈ1ЃЉЧѓжЄЃКVBЁЮЦНУцMOCЃЛ
ЃЈ2ЃЉЧѓжЄЃКЦНУцMOCЁЭЦНУцVAB
ЃЈ3ЃЉЧѓШ§РтзЖVЉABCЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕу.
СНЕу.
ЃЈ1ЃЉЧѓжЄЃКЁАШчЙћжБЯп![]() Й§Еу
Й§Еу![]() ЃЌФЧУД
ЃЌФЧУД![]() ЁБЪЧецУќЬтЃЛ
ЁБЪЧецУќЬтЃЛ
ЃЈ2ЃЉаДГіЃЈ1ЃЉжаУќЬтЕФФцУќЬтЃЌХаЖЯЫќЪЧецУќЬтЛЙЪЧМйУќЬтЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМИИіУќЬт
ЂйЗНГЬ![]() гавЛИіе§ЪЕИљЃЌвЛИіИКЪЕИљЃЌдђ
гавЛИіе§ЪЕИљЃЌвЛИіИКЪЕИљЃЌдђ![]() ЃЛ
ЃЛ
ЂкКЏЪ§![]() ЪЧХМКЏЪ§ЃЌЕЋВЛЪЧЦцКЏЪ§ЃЛ
ЪЧХМКЏЪ§ЃЌЕЋВЛЪЧЦцКЏЪ§ЃЛ
ЂлУќЬтЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБЕФЗёУќЬтЮЊЁАШє
ЁБЕФЗёУќЬтЮЊЁАШє![]() ЃЌдђ
ЃЌдђ![]() ЁБЃЛ
ЁБЃЛ
ЂмУќЬтЁА![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЁБЕФЗёЖЈЪЧЁА
ЁБЕФЗёЖЈЪЧЁА![]() ЃЌЖМга
ЃЌЖМга![]() ЁБЃЛ
ЁБЃЛ
ЂнЁА![]() ЁБЪЧЁА
ЁБЪЧЁА![]() ЁБЕФГфЗжВЛБивЊЬѕМўЃЎ
ЁБЕФГфЗжВЛБивЊЬѕМўЃЎ
е§ШЗЕФЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФУцЬх![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]()

ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ;
;
ЃЈ2ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§f(x)ЕФЖЈвхгђЮЊ(Ѓ2,2)ЃЌКЏЪ§g(x)ЃНf(xЃ1)ЃЋf(3Ѓ2x)ЃЎ
(1)ЧѓКЏЪ§g(x)ЕФЖЈвхгђЃЛ
(2)Шєf(x)ЪЧЦцКЏЪ§ЃЌЧвдкЖЈвхгђЩЯЕЅЕїЕнМѕЃЌЧѓВЛЕШЪНg(x)Ём0ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com