
【题目】已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x﹣y﹣2=0的距离为 ![]() ,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
(1)求抛物线C的方程;
(2)当点P(x0 , y0)为直线l上的定点时,求直线AB的方程;
(3)当点P在直线l上移动时,求|AF||BF|的最小值.
【答案】
(1)解:焦点F(0,c)(c>0)到直线l:x﹣y﹣2=0的距离 ![]() ,解得c=1,
,解得c=1,
所以抛物线C的方程为x2=4y.
(2)解:设 ![]() ,
, ![]() ,
,
由(1)得抛物线C的方程为 ![]() ,
, ![]() ,所以切线PA,PB的斜率分别为
,所以切线PA,PB的斜率分别为 ![]() ,
, ![]() ,
,
所以PA: ![]() ①PB:
①PB: ![]() ②
②
联立①②可得点P的坐标为 ![]() ,即
,即 ![]() ,
, ![]() ,
,
又因为切线PA的斜率为 ![]() ,整理得
,整理得 ![]() ,
,
直线AB的斜率 ![]() ,
,
所以直线AB的方程为 ![]() ,
,
整理得 ![]() ,即
,即 ![]() ,
,
因为点P(x0,y0)为直线l:x﹣y﹣2=0上的点,所以x0﹣y0﹣2=0,即y0=x0﹣2,
所以直线AB的方程为x0x﹣2y﹣2y0=0.
(3)解:根据抛物线的定义,有 ![]() ,
, ![]() ,
,
所以 ![]() =
= ![]() ,
,
由(2)得x1+x2=2x0,x1x2=4y0,x0=y0+2,
所以 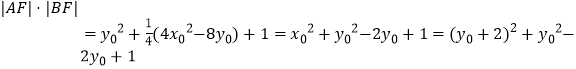 =
= ![]() .
.
所以当 ![]() 时,|AF||BF|的最小值为
时,|AF||BF|的最小值为 ![]()
【解析】(1)利用焦点到直线l:x﹣y﹣2=0的距离建立关于变量c的方程,即可解得c,从而得出抛物线C的方程;(2)先设 ![]() ,
, ![]() ,由(1)得到抛物线C的方程求导数,得到切线PA,PB的斜率,最后利用直线AB的斜率的不同表示形式,即可得出直线AB的方程;(3)根据抛物线的定义,有
,由(1)得到抛物线C的方程求导数,得到切线PA,PB的斜率,最后利用直线AB的斜率的不同表示形式,即可得出直线AB的方程;(3)根据抛物线的定义,有 ![]() ,
, ![]() ,从而表示出|AF||BF|,再由(2)得x1+x2=2x0 , x1x2=4y0 , x0=y0+2,将它表示成关于y0的二次函数的形式,从而即可求出|AF||BF|的最小值.
,从而表示出|AF||BF|,再由(2)得x1+x2=2x0 , x1x2=4y0 , x0=y0+2,将它表示成关于y0的二次函数的形式,从而即可求出|AF||BF|的最小值.


科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(坐标系与参数方程选做题)
已知曲线C的参数方程为 ![]() (t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
(t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
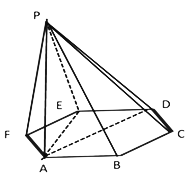
【题目】如图,已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①![]() ;
;
②直线![]() 平面
平面![]() ;
;
③平面![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的有_______(把所有正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
表中![]() ,
,![]() .
.
为了预测印刷20千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中选择的模型,求![]() 关于
关于![]() 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如下表所示:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀,则有多少把握认为学生的数学成绩与物理成绩有关系( )
A. 95% B. 97.5% C. 99.5% D. 99.9%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com