
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
科目:高中数学 来源: 题型:
【题目】如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.
(Ⅰ)证明:AE∥CD;
(Ⅱ)若圆O的半径为5,且PC=CF=FD=3,求四边形PBFA的外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.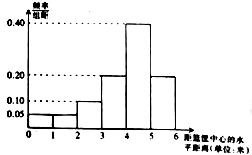
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,各个侧面均是边长为
中,各个侧面均是边长为![]() 的正方形,
的正方形,![]() 为线段
为线段![]() 的中点.
的中点.
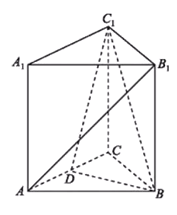
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)设![]() 为线段
为线段![]() 上任意一点,在
上任意一点,在![]() 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019迎新年联欢会上,为了活跃大家气氛,设置了“摸球中奖”游戏,桌子上放置一个不透明的箱子,箱子中有3个黄色、3个白色的乒乓球(其体积、质地完全相同)游戏规则:从箱子中随机摸出3个球,若摸得同一颜色的3个球,摸球者中奖价值50元奖品;若摸得非同一颜色的3个球,摸球者中奖价值20元奖品.
(1)摸出的3个球为白球的概率是多少?
(2)假定有10人次参与游戏,试从概率的角度估算一下需要准备多少元钱购买奖品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+ ![]() )的图象上所有的点( )
)的图象上所有的点( )
A.向右平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动 ![]() 个单位长度
个单位长度
D.向左平移移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据相关规定,24小时内的降水量为日降水量(单位:mm),不同的日降水量对应的降水强度如表:
日降水量 | (0,10) | [10,25) | [25,50) | [50,100) | [100,250) | [250,+∞) |
降水强度 | 小雨 | 中雨 | 大雨 | 暴雨 | 大暴雨 | 特大暴雨 |
为分析某市“主汛期”的降水情况,从该市2015年6月~8月有降水记录的监测数据中,随机抽取10天的数据作为样本,具体数据如下:
16 12 23 65 24 37 39 21 36 68
(1)请完成以如表示这组数据的茎叶图; 
(2)从样本中降水强度为大雨以上(含大雨)天气的5天中随机选取2天,求恰有1天是暴雨天气的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com