
【题目】已知函数f(x)=3x2+bx+c,不等式f(x)>0的解集为(﹣∞,﹣2)∪(0,+∞).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+mx﹣2在(2,+∞)上单调递增,求实数m的取值范围.
【答案】
(1)解:∵不等式f(x)>0的解集为(﹣∞,﹣2)∪(0,+∞).
∴ ![]() ,
,
解得 ![]() ,
,
∴f(x)=3x2+6x;
(2)解:由(1)知,f(x)=3x2+6x,
∵g(x)=f(x)+mx﹣2,
∴g(x)=3x2+6x+mx﹣2,
=3[x+(1+ ![]() )]2﹣2﹣3×+(1+
)]2﹣2﹣3×+(1+ ![]() )2,
)2,
∵函数g(x)在(2,+∞)上单调递增,
∴﹣(1+ ![]() )≤2,
)≤2,
∴m≥﹣18;
∴实数m的取值范围为m≥﹣18
【解析】(1)根据题意判断出:﹣2和0是方程3x2+bx+c=0的两个实根,代入列出方程,求出b和c的值;(2)由(1)求出g(x)的解析式,再求出对称轴方程,根据条件和二次函数的单调性,列出不等式,求出m的范围
【考点精析】掌握二次函数的性质和解一元二次不等式是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;求一元二次不等式
上递减;求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了![]() 位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分
位市民对共享单车的情况逬行问卷调査,并根根据其满意度评分值(滿分![]() 分)制作的茎叶图如图所示:
分)制作的茎叶图如图所示:
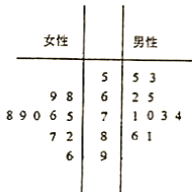
(1)分别计算男性打分的平均数和女性打分的中位数;
(2)从打分在![]() 分以下(不含
分以下(不含![]() 分)的市民抽取
分)的市民抽取![]() 人,求有女性被抽中的概率.
人,求有女性被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.y=sin(2x+ ![]() )
)
B.y=sin( ![]() x+
x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com