
【题目】已知甲乙两名篮球运动员每场比赛得分的原始记录用如下茎叶图表示:
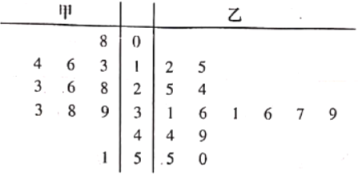
(1)按从小到大的顺序写出甲运动员的得分;
(2)分别求甲乙运动员得分的中位数;
(3)估计乙运动员在一场比赛中得分落在![]() 内的概率.
内的概率.
【答案】(1) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(2)
.(2)![]() ,
, ![]() (3)
(3)![]()
【解析】
(1)利用茎叶图能按从小到大的顺序写出甲运动员的得分.
(2)是茎叶图和中位数定义能求出甲、乙运动员得分的中位数.
(3)由茎叶图统计数字得到乙运动员有14次得分记录中有10次分落在[10,40]内,由此能求出乙运动员在一场比赛中得分落在[10,40]内的概率.
(1)按从小到大的顺序写出甲运动员的得分为:
8,13,14,16,23,26,28,33,38,39,51.
(2)甲运动员11次得分记录的中位数是26.
乙运动员14次得分记录按从小到大排在7、8两位的数字都为36,
∴乙运动员得分的中位数是36.
(3)由茎叶图统计数字得到乙运动员有14次得分记录中有10次分落在[10,40]内,
∴乙运动员在一场比赛中得分落在[10,40]内的概率![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
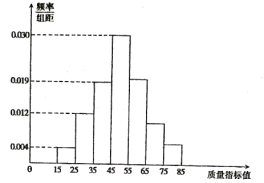
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋内装的红白黑球分别有![]() ,
,![]() ,
,![]() 个,从中任取两个球,则互斥而不对立的事件是( )
个,从中任取两个球,则互斥而不对立的事件是( )
A.至少一个白球;都是白球B.至少一个白球;至少一个黑球
C.至少一个白球;一个白球一个黑球D.至少一个白球;红球黑球各一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:

其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,![]() 代表“生活不能自理”,按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位,则被访问地3位老龄人中恰有1位老龄人的健康指数不大于0的概率为___
代表“生活不能自理”,按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位,则被访问地3位老龄人中恰有1位老龄人的健康指数不大于0的概率为___
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com