[题目]已知函数f(x)=ax﹣1.当x∈＞0.且函数g﹣4的图象不过第二象限.则a的取值范围是( )A.B.C.(1.3]D.(1.5] 题目和参考答案——青夏教育精英家教网—

【题目】已知函数f（x）=ax﹣1（a＞0，且a≠1），当x∈（0，+∞）时，f（x）＞0，且函数g（x）=f（x+1）﹣4的图象不过第二象限，则a的取值范围是（）
A.（1，+∞）
B.
C.（1，3]
D.（1，5]

【答案】D
【解析】解：当a＞1时，函数f（x）在（0，+∞）上单调递增，f（x）=ax﹣1＞0；
当0＜a＜1时，函数f（x）在（0，+∞）上单调递减，f（x）=ax﹣1＜0，舍去．
故a＞1．
∵函数g（x）=f（x+1）﹣4的图象不过第二象限，
∴g（0）=a1﹣5≤0，
∴a≤5，
∴a的取值范围是（1，5]．
故选：D．
对a分类讨论：利用指数函数的单调性可得a＞1．由于函数g（x）=ax+1﹣5的图象不过第二象限，可得g（0）≤0，求解即可得答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2 ，BC=4 ，PA=2，点M在线段PD上．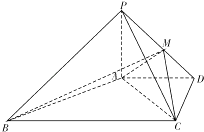

（1）求证：AB⊥PC．
（2）若二面角M﹣AC﹣D的大小为45°，求BM与平面PAC所成的角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=lnx．
（1）求函数g（x）=f（x+1）﹣x的最大值；
（2）若对任意x＞0，不等式f（x）≤ax≤x2+1恒成立，求实数a的取值范围；
（3）若x1＞x2＞0，求证：＞．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2+2ax+2，x∈[﹣5，5]．
（1）当a=﹣1时，求函数f（x）的单调递增区间；
（2）求实数a的取值范围，使y=f（x）在区间[﹣5，5]上是单调函数．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=tx，（x∈R）．
（1）若t=ax+b，a，b∈R，且﹣1≤f（﹣1）≤2，2≤f（1）≤4，求点（a，b）的集合表示的平面区域的面积；
（2）若t=2+ ，（x＜1且x≠0），求函数f（x）的最大值；
（3）若t=x﹣a﹣3（a∈R），不等式b2+c2﹣bc﹣3b﹣1≤f（x）≤a+4（b，c∈R）的解集为[﹣1，5]，求b，c的值．