
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( )
A.[﹣2,2]
B.[2,+∞)
C.[0,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
【答案】B
【解析】解:令g(x)=f(x)﹣ ![]() x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣
x2 , ∵g(﹣x)+g(x)=f(﹣x)﹣ ![]() x2+f(x)﹣
x2+f(x)﹣ ![]() x2=0,
x2=0,
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,g′(x)=f′(x)﹣x<0,
故函数g(x)在(0,+∞)上是减函数,故函数g(x)在(﹣∞,0)上也是减函数,
由f(0)=0,可得g(x)在R上是减函数,
∴f(4﹣m)﹣f(m)=g(4﹣m)+ ![]() (4﹣m)2﹣g(m)﹣
(4﹣m)2﹣g(m)﹣ ![]() m2=g(4﹣m)﹣g(m)+8﹣4m≥8﹣4m,
m2=g(4﹣m)﹣g(m)+8﹣4m≥8﹣4m,
∴g(4﹣m)≥g(m),∴4﹣m≤m,解得:m≥2,
故选:B.
令g(x)=f(x)﹣ ![]() x2 , 由g(﹣x)+g(x)=0,可得函数g(x)为奇函数.利用导数可得函数g(x)在R上是减函数,f(4﹣m)﹣f(m)≥8﹣4m,即g(4﹣m)≥g(m),可得 4﹣m≤m,由此解得a的范围.
x2 , 由g(﹣x)+g(x)=0,可得函数g(x)为奇函数.利用导数可得函数g(x)在R上是减函数,f(4﹣m)﹣f(m)≥8﹣4m,即g(4﹣m)≥g(m),可得 4﹣m≤m,由此解得a的范围.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为![]() ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为![]() ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量![]() 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果![]() 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分![]() 的分布列和数学期望E
的分布列和数学期望E![]() ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 满足
满足![]() ,且在定义域内
,且在定义域内![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosωx(sinωx+ ![]() cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(6,﹣3),
=(6,﹣3), ![]() =(5﹣x,﹣3﹣y),
=(5﹣x,﹣3﹣y), ![]() =(4,1)
=(4,1)
(1)若四边形ABCD是平行四边形,求x,y的值;
(2)若△ABC为等腰直角三角形,且∠B为直角,求x,y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位有50名职工,现要从中抽取 10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(Ⅰ)若第5组抽出的号码为22,写出所有被抽出职工的号码;
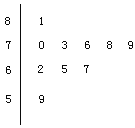
(Ⅱ)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的平均数、中位数和方差;
(Ⅲ)在(Ⅱ)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(![]() 73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 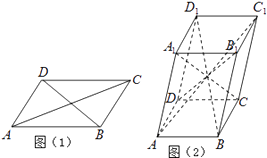
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点. (Ⅰ)若 ![]() ,求直线AB的斜率;
,求直线AB的斜率;
(Ⅱ)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.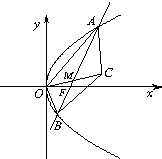
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com