
【题目】编号为 ![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12] | 31 | 38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
区间 |
|
|
|
人数 |
(Ⅱ)从得分在区间 ![]() 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.
【答案】解:(Ⅰ)解:4,6,6
(Ⅱ)(i)解:得分在区间 ![]() 内的运动员编号为
内的运动员编号为 ![]() 从中随机
从中随机
抽取2人,所有可能的抽取结果有:![]() ,
,![]() 共15种。
共15种。
(ii)解:“从得分在区间 ![]() 内的运动员中随机抽取2人,这2人得分之和大于50”(记为事件B)的所有可能结果有:
内的运动员中随机抽取2人,这2人得分之和大于50”(记为事件B)的所有可能结果有: ![]() ,共5种。
,共5种。
所以 ![]()
【解析】(I)根据题目中所给的条件的特点,根据16名篮球运动员在某次训练比赛中的得分记录表,易得出得分在对应区间内的人数.
(II)(i)根据(I)的结论,列出在区间[20,30)内的运动员中随机抽取2人所有可能的抽取结果;
(ii)列出这2人得分之和大于50分的基本事件的个数,代入古典概型公式即可得到答案.
主要考查用列举法计算随机事件所含的基本事件、古典概型及其概率计算公式等基础知识,古典概型由于满足基本事件的有限性和基本事件发生的等可能性这两个重要特征,所以求事件的概率就可以不通过大量的重复试验,而只要通过对一次试验中可能出现的结果进行分析和计算即可.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆 ![]() :
: ![]() (
( ![]() )与直线
)与直线 ![]() :
: ![]() 相切,设点
相切,设点 ![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于 ![]() ,且动点
,且动点 ![]() 满足
满足 ![]() ,设动点
,设动点 ![]() 的轨迹为曲线
的轨迹为曲线 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)直线 ![]() 与直线
与直线 ![]() 垂直且与曲线
垂直且与曲线 ![]() 交于
交于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )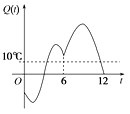
A.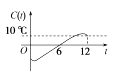
B.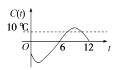
C.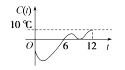
D.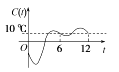
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?” 意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系. 曲线
轴正半轴为极轴建立极坐标系. 曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,
, ![]() 为曲线
为曲线 ![]() 上异于极点的动点,点
上异于极点的动点,点 ![]() 在射线
在射线 ![]() 上,且
上,且 ![]() 成等比数列.
成等比数列.
(Ⅰ)求点 ![]() 的轨迹
的轨迹 ![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知 ![]() ,
, ![]() 是曲线
是曲线 ![]() 上的一点且横坐标为
上的一点且横坐标为 ![]() ,直线
,直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,试求
两点,试求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com