
【题目】读下面的程序:
i=1
S=0
DO
INPUT x
S=S+x
i=i+1
LOOP UNTIL i>10
A=S/10
PRINT A
END
该程序的作用是
A. 计算9个数的和 B. 计算9个数的平均数
C. 计算10个数的和 D. 计算10个数的平均数
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当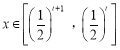 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
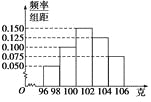
A. 90 B. 75 C. 60 D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算数平方根成正比,已知投资1万元时两类产品的收益分别是0.125万元和0.5万元(如图).
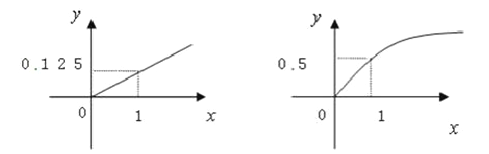
(1) 分别写出两种产品的收益与投资的函数关系;
(2) 该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形. ①、②、③组合成“三段论”.根据“三段论”推理出一个结论,则这个结论是( )
A. 正方形是平行四边形 B. 平行四边形的对角线相等
C. 正方形的对角线相等 D. 以上均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.

(1)求证:BE∥平面PAD;
(2)若AP=2AB,求证:BE⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com