
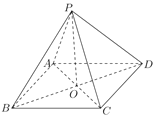
【题目】已知四棱锥![]() 的底面
的底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() 底面
底面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的值;
的值;
(3)求平面![]() 与平面
与平面![]() 所成二面角
所成二面角![]() 的值.(用反三角函数表示)
的值.(用反三角函数表示)
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由已知中四棱锥PABCD的底面ABCD为菱形,且∠ABC=60°,PB=PD=AB=2,PA=PC,AC与BD相交于点O,根据平行四边形两条对角线互相平分及等腰三角形三线合一,结合线面垂直的判定定理,我们易得到结论;
(2)以O为坐标原点,建立坐标系,分别求出各顶点坐标,进而求出直线PB的方向向量与平面PCD的法向量,代入线面夹角的向量法公式,即可求出答案;
(3)求出平面![]() 的法向量,代入面面夹角的向量法公式,即可求出答案.
的法向量,代入面面夹角的向量法公式,即可求出答案.
(1)证明:因为ABCD为菱形,
所以O为AC,BD的中点
因为PB=PD,PA=PC,
所以PO⊥BD,PO⊥AC
所以PO⊥底面ABCD;
(2)解:因为ABCD为菱形,所以AC⊥BD,
建立如图所示空间直角坐标系
又∠ABC=60°,PA=AB=2
得![]() ,
,
所以![]()
则![]() ,
,
设平面PCD的法向量![]()
有 ,所以
,所以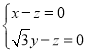 ,令
,令![]()
得![]() ,
, ,
,
直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的值为
的值为![]() ;
;

(3)设平面![]() 的法向量
的法向量![]() ,
,
因为![]()
有 ,所以
,所以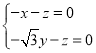 ,令
,令![]()
得![]() ,
,
 ,
,
由图知,平面![]() 与平面
与平面![]() 所成二面角为钝角,
所成二面角为钝角,
![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,直线
为顶点,直线![]() 为准线的抛物线.以坐标原点
为准线的抛物线.以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)分别求出直线![]() 与曲线
与曲线![]() 的极坐标方程:
的极坐标方程:
(2)点![]() 是曲线
是曲线![]() 上位于第一象限内的一个动点,点
上位于第一象限内的一个动点,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,且
上位于第二象限内的一个动点,且![]() ,请求出
,请求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(Ⅰ)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅱ)设![]() 在(0,2)内恰有两个极值点,求实数
在(0,2)内恰有两个极值点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,方程
,方程![]() 在区间
在区间![]() 有解,求实数
有解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
![]() 如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
如果随机调查这个班的一名学生,求事件A:抽到不积极参加班级工作且学习积极性不高的学生的概率;
![]() 若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,请用字母代表不同的学生列举出抽取的所有可能结果;
若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,请用字母代表不同的学生列举出抽取的所有可能结果;
![]() 在
在![]() 的条件下,求事件B:两名学生中恰有1名男生的概率.
的条件下,求事件B:两名学生中恰有1名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com