
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,证明:函数
时,证明:函数![]() 有两个零点;
有两个零点;
(Ⅲ)若函数![]() 有两个不同的极值点,记作
有两个不同的极值点,记作![]() ,且
,且![]() ,证明
,证明![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
上单调递增;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)求得函数的导数,分类讨论,即可求解函数的单调区间;
(Ⅱ)当![]() 时,由(Ⅰ)知函数
时,由(Ⅰ)知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,求得函数的最小值
上单调递增,求得函数的最小值![]() ,记
,记![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最值,利用零点的存在定理,即可求解;
的单调性与最值,利用零点的存在定理,即可求解;
(Ⅲ)求得![]() ,得到
,得到![]() ,把欲证
,把欲证![]() 转化为证
转化为证![]() ,进而得到
,进而得到 ,设
,设![]() ,等价于
,等价于![]() ,令
,令![]() ,利用导数求得函数的单调性,即可求解.
,利用导数求得函数的单调性,即可求解.
(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,
由![]() ,可得
,可得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;
单调递增;
当![]() 时,即
时,即![]() 时,函数
时,函数![]() 单调递减.
单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)当![]() 时,由(Ⅰ)知函数
时,由(Ⅰ)知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .取
.取![]() ,
,
记![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减. ![]() .所以当
.所以当![]() ,
,
![]() ,所以函数
,所以函数![]() 在
在![]() 上存在一个零点.当
上存在一个零点.当![]() 时,
时,![]() ,
,![]() ,所以函数
,所以函数![]() 在
在![]() 上存在一个零点.所以,当
上存在一个零点.所以,当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
(Ⅲ)依题意得,![]() ,则
,则![]() ,
,
因为![]() 有两个极值点
有两个极值点![]() ,所以
,所以![]() ,
,
欲证![]() 等价于证
等价于证![]() ,即
,即![]() ,所以
,所以![]() ,
,
因为![]() ,所以原不等式等价于
,所以原不等式等价于![]() ①,
①,
由![]() 可得
可得![]() ,则
,则 ②,
②,
由①②可知,原不等式等价于 ,即
,即 ,
,
设![]() ,则上式等价于
,则上式等价于![]() 时,
时,![]() ,
,
令![]() ,则
,则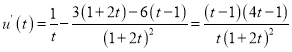 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以原不等式成立,即![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示
年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )
日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )

A.![]() 月下旬新增确诊人数呈波动下降趋势
月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,![]() 月下旬单日治愈人数超过确诊人数
月下旬单日治愈人数超过确诊人数
C.![]() 月
月![]() 日至
日至![]() 月
月![]() 日新增确诊人数波动最大
日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在![]() 月
月![]() 日左右达到峰值
日左右达到峰值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣ax﹣xlnx.其中a∈R.
(Ⅰ)若![]() ,证明:f(x)≥0;
,证明:f(x)≥0;
(Ⅱ)若xe1﹣x≥1﹣f(x)在x∈(1,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有编号分别为1,2,3,4,5,6,7,8的八个小球和编号为1,2,3,4,5,6,7,8的八个盒子.现将这八个小球随机放入八个盒子内,要求每个盒子内放一个球,要求编号为偶数的小球在编号为偶数的盒子内,且至少有四个小球在相同编号的盒子内,则一共有______种投放方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆Q:(x+2)2+(y-2)2=1,抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A,B两点,过F且与l垂直的直线l'与圆Q有交点.

(1)求直线l'的斜率的取值范围;
(2)求△AOB面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com