
分析 根据题意,画出单位圆,得出单位圆中cosθ=$\overrightarrow{OM}$,sinθ=$\overrightarrow{MA}$,再根据不等式求出θ的取值范围.
解答 解:(1)根据题意,画出图形,如图所示,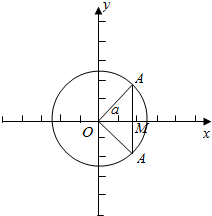
在单位圆中cosθ=$\overrightarrow{OM}$,
且cosθ<$\frac{\sqrt{2}}{2}$在[0,2π]的角是$\frac{π}{4}$<θ<$\frac{7π}{4}$,
∴θ的取值范围是:$\frac{π}{4}$+2kπ<θ<$\frac{7π}{4}$+2kπ,k∈Z;
(2)根据题意,画出图形,如图2所示,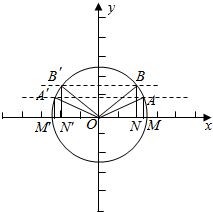
在单位圆中,sinθ=$\overrightarrow{MA}$,
∴$\frac{1}{2}$≤sinθ<$\frac{\sqrt{3}}{2}$在[0,2π]的角是$\frac{π}{6}$≤θ<$\frac{π}{3}$,或$\frac{2π}{3}$<θ≤$\frac{5π}{6}$,
∴θ的取值范围是:$\frac{π}{6}$+2kπ≤θ<$\frac{π}{3}$+2kπ,或$\frac{2π}{3}$+2kπ<θ≤$\frac{5π}{6}$+2kπ,k∈Z.
点评 本题考查了利用单位圆中的三角函数线求满足条件的角的集合的应用问题,是基础题目.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com