
| A. | [-1,0] | B. | [-1,2] | C. | [-1,3] | D. | [-1,4] |
分析 如图所示,由题意可得:点M所在的圆的方程为:(x-1)2+(y-1)2≤1(0≤x≤2,0≤y≤2).可设点M(x,y)可得$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x-1)2+y2-1,由$\sqrt{(x-1)^{2}+{y}^{2}}$∈[0,2],即可得出.
解答  解:如图所示,
解:如图所示,
由题意可得:点M所在的圆的方程为:(x-1)2+(y-1)2≤1(0≤x≤2,0≤y≤2).
可设点M(x,y)
A(0,0),B(2,0).
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=(-x,-y)•(2-x,-y)=-x(2-x)+y2=(x-1)2+y2-1,
由$\sqrt{(x-1)^{2}+{y}^{2}}$∈[0,2],
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$∈[-1,3],
故选:C.
点评 本题考查了圆的标准方程、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{7π}{6}$ | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
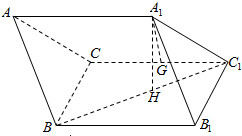 在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.
在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{6}$ | B. | 4$+\sqrt{3}$ | C. | 4$+2\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
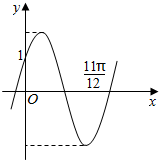 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com