
【题目】在极坐标系中,曲线 ![]() 的极坐标方程分别为
的极坐标方程分别为 ![]() ,
, ![]() .
.
(1)求曲线 ![]() 和
和 ![]() 的公共点的个数;
的公共点的个数;
(2)过极点作动直线与曲线 ![]() 相交于点Q,在OQ上取一点P,使
相交于点Q,在OQ上取一点P,使 ![]()
![]() ,求点P的轨迹,并指出轨迹是什么图形.
,求点P的轨迹,并指出轨迹是什么图形.
【答案】
(1)解: ![]() 的直角坐标方程为
的直角坐标方程为 ![]() ,它表示圆心为
,它表示圆心为 ![]() ,半径为1的圆,
,半径为1的圆, ![]() 的直角坐标方程为
的直角坐标方程为 ![]() ,所以曲线
,所以曲线 ![]() 为直线,由于圆心到直线的距离为
为直线,由于圆心到直线的距离为 ![]() ,所以直线与圆相离,即曲线
,所以直线与圆相离,即曲线 ![]() 和
和 ![]() 的公共点个数为0
的公共点个数为0
(2)解:设 ![]() ,
, ![]() ,则
,则 ![]() 即
即 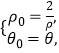 ①
①
因为点 ![]() 在曲线
在曲线 ![]() 上,所以
上,所以 ![]() ,②
,②
将①代入②,得 ![]() ,即
,即 ![]() ,此即为点P的轨迹方程,化为直角坐标方程为
,此即为点P的轨迹方程,化为直角坐标方程为 ![]() ,
,
因此,点P的轨迹是以 ![]() 为圆心,1为半径的圆
为圆心,1为半径的圆
【解析】1.根据ρ sin θ = y、ρ cos θ = x、.ρ2=x 2 + y 2化解出直角坐标方程;2.![]() 根据圆心到直线的距离与圆的半径比较确定直线与圆的位置关系即可得出答案;3.根据已知条件列出关系式,再根据C 2的极坐标方程确定点P的轨迹方程,最后根据P的极坐标方程转化为直角坐标方程确定轨迹图形。
根据圆心到直线的距离与圆的半径比较确定直线与圆的位置关系即可得出答案;3.根据已知条件列出关系式,再根据C 2的极坐标方程确定点P的轨迹方程,最后根据P的极坐标方程转化为直角坐标方程确定轨迹图形。


科目:高中数学 来源: 题型:
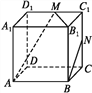
【题目】如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;②直线AM与BN是平行直线;
③直线BN与MB1是异面直线; ④直线MN与AC所成的角为60°.
其中正确的结论为___ (注:把你认为正确的结论序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 计算得
计算得 ![]()
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C.有99%以上的把握认为“爱好该项运动与性别无关”
D.有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当 ![]() 时,求
时,求 ![]() 的单调区间;
的单调区间;
(2)设 ![]() ,
, ![]() 是曲线
是曲线 ![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线 ![]() 的斜率
的斜率 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围;
的取值范围;
(3)设函数 ![]() 有两个极值点
有两个极值点 ![]() ,
, ![]() ,且
,且 ![]() ,若
,若 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标中,直线l的方程为 ![]() ,曲线C的方程为
,曲线C的方程为 ![]() .
.
(1)求直线l与极轴的交点到极点的距离;
(2)若曲线C上恰好有两个点到直线l的距离为 ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,![]() ,
,![]() ,F分别为AB,PC的中点.
,F分别为AB,PC的中点.
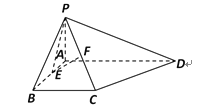
(I)若四棱锥P-ABCD的体积为4,求PA的长;
(II)求证:PE⊥BC;
(III)求PC与平面PAD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com