
【题目】已知动圆![]() 过定点
过定点![]() ,且圆心
,且圆心![]() 到直线
到直线![]() 的距离比
的距离比![]() 大
大![]() .
.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知轨迹![]() 与直线
与直线![]() 相交于
相交于![]() 两点.试问,在
两点.试问,在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得
使得![]() 是一个定值?如果存在,求出定点
是一个定值?如果存在,求出定点![]() 的坐标和这个定值;如果不存在,请说明理由.
的坐标和这个定值;如果不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着
绕着![]() 翻折到
翻折到![]() .
.
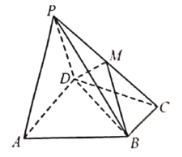
(1)![]() 为
为![]() 上一点,且
上一点,且![]() ,当
,当![]() 平面
平面![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)当平面![]() 与平面
与平面![]() 所成的锐二面角大小为
所成的锐二面角大小为![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦.
所成角的正弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
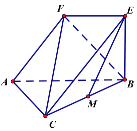
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角正弦值为
所成的角正弦值为![]() ,若存在求出
,若存在求出![]() 的长,若不存在说明理由.
的长,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中所有棱长都相等,
中所有棱长都相等,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.现有下列四个结论:
的中点.现有下列四个结论:
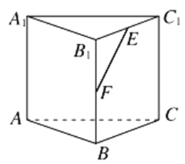
![]() ;
;![]() ;
;
![]() 平面
平面![]() ;
;![]() 异面直线
异面直线![]() 与
与![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
其中正确的结论是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖冲之是中国南北朝时期的数学家和天文学家,他在数学方面的突出贡献是将圆周率的精确度计算到小数点后第![]() 位,也就是
位,也就是![]() 和
和![]() 之间,这一成就比欧洲早了
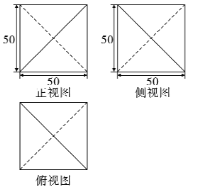
之间,这一成就比欧洲早了![]() 多年,我校“爱数学”社团的同学,在祖冲之研究圆周率的方法启发下,自制了一套计算圆周率的数学实验模型.该模型三视图如图所示,模型内置一个与其各个面都相切的球,该模型及其内球在同一方向有开口装置.实验的时候,同学们随机往模型中投掷大小相等,形状相同的玻璃球,通过计算落在球内的玻璃球数量,来估算圆周率的近似值.已知某次实验中,某同学一次投掷了
多年,我校“爱数学”社团的同学,在祖冲之研究圆周率的方法启发下,自制了一套计算圆周率的数学实验模型.该模型三视图如图所示,模型内置一个与其各个面都相切的球,该模型及其内球在同一方向有开口装置.实验的时候,同学们随机往模型中投掷大小相等,形状相同的玻璃球,通过计算落在球内的玻璃球数量,来估算圆周率的近似值.已知某次实验中,某同学一次投掷了![]() 个玻璃球,请你根据祖冲之的圆周率精确度(取小数点后三位)估算落在球内的玻璃球数量( )
个玻璃球,请你根据祖冲之的圆周率精确度(取小数点后三位)估算落在球内的玻璃球数量( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二项式![]() 的二项式系数和为256.
的二项式系数和为256.
(1)求展开式中二项式系数最大的项;
(2)求展开式中各项的系数和;
(3)展开式中是否有有理项,若有,求系数;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 底面
底面![]() ,则下列结论中正确结论的序号是_________________.
,则下列结论中正确结论的序号是_________________.
①![]() ;②
;②![]() 平面
平面![]() ;③
;③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角;④
所成的角;④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级的数学兴趣小组釆取抽签方式随机分成甲、乙两个小组进行数学解题对抗赛.每组各20人,根据各位学生在第三次数学解题对抗赛中的解题时间(单位:秒)绘制了如下茎叶图:

(1)请评出第三次数学对抗赛的优胜小组,并求出这40位学生完成第三次数学解题对抗赛所需时间的中位数![]() ;
;
(2)对于(1)中的中位数![]() ,根据这40位学生完成第三次数学对抗赛所需时间超过
,根据这40位学生完成第三次数学对抗赛所需时间超过![]() 和不超过
和不超过![]() 的人数,完成下面的列联表,并判断能否有
的人数,完成下面的列联表,并判断能否有![]() 的把握认为甲、乙两个小组在此次的数学对抗赛中的成绩有差异?
的把握认为甲、乙两个小组在此次的数学对抗赛中的成绩有差异?
超过 | 不超过 | 总计 | |
甲组 | |||
乙组 | |||
总计 |
附: ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com