
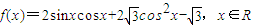 .
.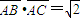 ,,求△ABC的面积.
,,求△ABC的面积.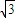 ,利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,
,利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,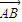 •
•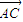 =
=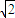 ,得到|
,得到|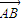 |•|
|•|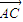 |的值,再由sinA的值,利用三角形的面积公式即可求出三角形ABC的面积.
|的值,再由sinA的值,利用三角形的面积公式即可求出三角形ABC的面积.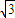 (2cos2x-1)=sin2x+
(2cos2x-1)=sin2x+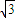 cos2x=2sin(2x+
cos2x=2sin(2x+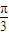 ),
),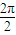 =π;
=π;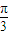 )≤1,即-2≤2sin(2x+
)≤1,即-2≤2sin(2x+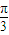 )≤2,
)≤2,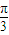 )=1,
)=1,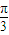 )=
)= ,
,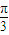 =
=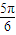 ,即A=
,即A=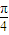 ,
,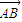 •
•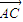 =|
=|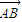 |•|
|•|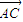 |cosA=
|cosA=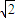 ,
,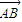 |•|
|•|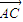 |=2,
|=2, |
|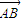 |•|
|•|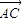 |sinA=
|sinA=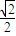 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年湖北省荆州市高三(上)12月质量检查数学试卷Ⅰ(理科)(解析版) 题型:解答题
 .
. ,,求△ABC的面积.
,,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市临沭县高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012年天津市河北区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com