
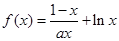 .
.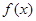 在
在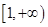 上是增函数,求正实数
上是增函数,求正实数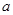 的取值范围;
的取值范围;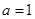 ,
,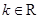 且
且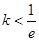 ,设
,设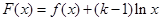 ,求函数
,求函数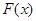 在
在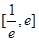 上的最大值和最小值.
上的最大值和最小值.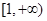 ;(Ⅱ)当
;(Ⅱ)当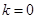 时,
时,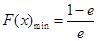 ,
,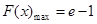 ;当
;当 且
且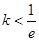 时,
时,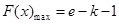 ,
,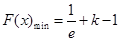 .
.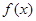 在
在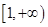 上是增函数可知
上是增函数可知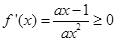 在
在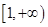 恒成立,从而确定
恒成立,从而确定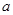 的取值范围;(Ⅱ)先求出
的取值范围;(Ⅱ)先求出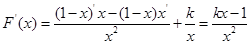 ,然后分
,然后分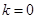 和
和 两类进行讨论,从而得出函数
两类进行讨论,从而得出函数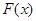 在
在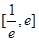 上的最大值和最小值.注意化归转化和分类讨论的数学思想方法的运用.
上的最大值和最小值.注意化归转化和分类讨论的数学思想方法的运用.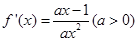 ,因为函数
,因为函数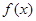 在
在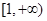 上是增函数,
上是增函数,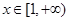 时,不等式
时,不等式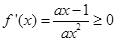 即
即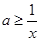 恒成立----2分
恒成立----2分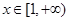 时,
时,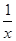 的最大值为
的最大值为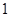 ,则实数
,则实数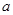 的取值范围是
的取值范围是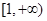 -----4分
-----4分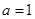 ,
,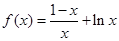 ,
,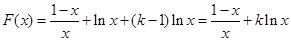
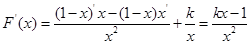 6分
6分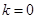 ,则
,则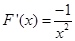 ,在
,在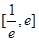 上, 恒有
上, 恒有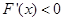 ,所以
,所以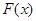 在
在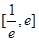 上单调递减
上单调递减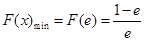 ,
,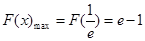 7分
7分 时
时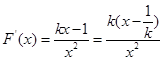
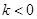 ,在
,在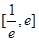 上,恒有
上,恒有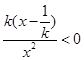 ,所以
,所以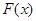 在
在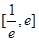 上单调递减,
上单调递减,
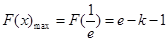 10分
10分 时,因为
时,因为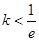 ,所以
,所以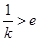 ,
,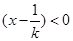 ,所以
,所以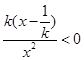 ,
,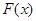 在
在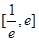 上单调递减
上单调递减
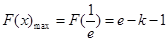 12分
12分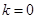 时,
时,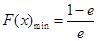 ,
,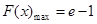 ;
; 且
且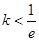 时,
时,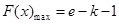 ,
,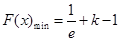 . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
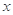 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为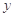 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用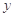 随每年改造生态环境总费用
随每年改造生态环境总费用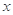 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少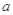 亿元,至多
亿元,至多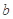 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用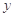 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用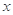 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用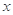 的25%.
的25%.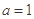 ,
,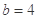 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=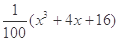 作为生态环境改造投资方案.
作为生态环境改造投资方案.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
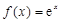 ,点
,点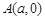 为一定点,直线
为一定点,直线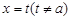 分别与函数
分别与函数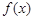 的图象和
的图象和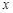 轴交于点
轴交于点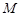 ,
,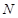 ,记
,记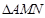 的面积为
的面积为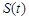 .
.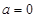 时,求函数
时,求函数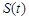 的单调区间;
的单调区间;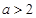 时, 若
时, 若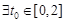 ,使得
,使得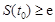 , 求实数
, 求实数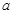 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com