
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.

(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2=
+y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2= ![]() 相切于点W(O为坐标原点).
相切于点W(O为坐标原点).
(1)证明:OE⊥OF;
(2)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人相约于下午1:00~2:00之间到某车站乘公共汽车外出,他们到达车站的时间是随机的.设在下午1:00~2:00之间该车站有四班公共汽车开出,开车时间分别是1:15,1:30,1:45,2:00.求他们在下述情况下乘同一班车的概率:
(1)约定见车就乘;
(2)约定最多等一班车.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+ax+b,a,b∈R.
(1)若2a+b=4,证明:|f(x)|在区间[0,4]上的最大值M(a)≥12;
(2)存在实数a,使得当x∈[0,b]时,1≤f(x)≤10恒成立,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),且当x∈(0,4]时f(x)= ![]() ,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
A.(﹣ ![]() ln6,ln2]
ln6,ln2]
B.(﹣ln2,﹣ ![]() ln6)
ln6)
C.(﹣ln2,﹣ ![]() ln6]
ln6]
D.(﹣ ![]() ln6,ln2)
ln6,ln2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右准线方程为
的右准线方程为![]() ,又离心率为
,又离心率为![]() ,椭圆的左顶点为
,椭圆的左顶点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为椭圆上异于
为椭圆上异于![]() 任意一点.
任意一点.
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过点
经过点![]() 与点
与点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线所在的直线的方程.
的切线,求切线所在的直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求出线段![]() 的中点
的中点![]() ,进而得到线段
,进而得到线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,∴
,∴![]() .则圆
.则圆![]() 的方程可求
的方程可求
(2)当切线斜率不存在时,可知切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,由
,由![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,即可到切线所在直线的方程.
,即可到切线所在直线的方程.
试题解析:((1)设 线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,
,
∴线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,
,
∴![]() .
.
∴圆![]() 的方程为
的方程为![]() .
.
(2)当切线斜率不存在时,切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,即
,即![]() ,
,
则![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,∴切线方程为
,∴切线方程为![]() .
.
故满足条件的切线方程为![]() 或
或![]() .
.
【点睛】本题考查圆的方程的求法,圆的切线,中点弦等问题,解题的关键是利用圆的特性,利用点到直线的距离公式求解.
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
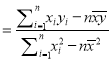 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com